Arsip 2021:

Agustus

Virtual Tour FMIPA UGM (360 Video)

Artikel Selasa, 31 Agustus 2021

Fakultas yang mengasuh Matematika dan Ilmu Pengetahuan Alam di Universitas Gadjah Mada diresmikan berdirinya pada tanggal 19 September 1955 dengan Surat Keputusan Menteri Pendidikan, Pengajaran dan Kebudayaan tanggal 15 September 1955 nomor 53759/Kab. Saat ini kampus FMIPA dijadikan satu yang berada di Sekip Utara Bulaksumur Yogyakarta. Di video ini kita akan diajak oleh salah satu mahasiswa matematika, yaitu Silvina Rosita Yulianti untuk keliling FMIPA UGM.

Pembahasan Soal 5 Relasi Rekurensi

Tutorial Selasa, 24 Agustus 2021

Soal Diberikan barisan \{a_{n}\} dengan relasi rekurensi a_{n+2}=4a_{n+1}-4a_{n} untuk n\geq 0 dan nilai awal a_{0}=3 dan a_{1}=7. Tentukan formula untuk a_n.

Pembahasan

Persamaan karakteristik yang bersesuaian adalah p(x) = x^{2}-4x+4. Diperoleh k = 2, m_{1} = 2, r_{1} = 2 yang menghasilkan

    \[ a_{n} = (A_{0}+A_{1}n)2^{n} .\]

Dari nilai awal, ketika disubstitusi menjadi

    \begin{equation*} \begin{split} 3 = a_{0} &= A_{0}\\ 10= a_{1}&=2A_{0}+2A_{1}. \end{split} \end{equation*}

Diperoleh

    \begin{equation*} A_{0}=3~\text{dan}~A_{1}=2. \end{equation*}

Jadi a_{n}=(A_{0}+A_{1}n)2^{n}=(3+2n)2^{n}=3\cdot2^{n}+n\cdot2^{n+1} untuk setiap n\geq 0.

Credit: Iwan Ernanto

Pembahasan Soal 4 Relasi Rekurensi

Tutorial Selasa, 24 Agustus 2021

Soal Diberikan barisan \{a_{n}\} dengan relasi rekurensi a_{n+2}=2a_{n+1}-a_{n} untuk n\geq 0 dan nilai awal a_{0}=3 dan a_{1}=7. Tentukan formula untuk a_n.

Pembahasan

Dapat dilihat persamaan karakteristik yang memenuhi adalah p(x) = x^{2}-2x+1. Diperoleh k = 2, m_{1} = 2, r_{1} = 1. Hal ini mengakibatkan

    \[ a_{n} = (A_{0}+A_{1}n)1^{n} .\]

    \begin{equation*} \begin{split} 3 = a_{0} &= A_{0}\\ 7= a_{1}&=A_{0}+A_{1}. \end{split} \end{equation*}

Diperoleh

    \begin{equation*} A_{0}=3~\text{dan}~A_{1}=4 . \end{equation*}

Jadi a_{n}=(A_{0}+A_{1}n)1^{n}=3+4n untuk setiap n\geq 0.

Credit: Iwan Ernanto

Pembahasan Soal 3 Relasi Rekurensi

Tutorial Senin, 23 Agustus 2021

Soal Diberikan barisan \{a_{n}\} dengan relasi rekurensi a_{n + 2} = 5a_{n+1}-4a_{n} untuk n\geq 0 dan a_{0} = 1, a_{2}=7. Tentukan formula untuk a_n.

Jawaban

Persamaan karakteristik yang dihasilkan adalah p(x) = x^{2}-5x+4. Diperoleh k = 2, m_{1} =m_{2}= 1, r_{1} = 1 dan r_{2}=4. Jadi formula untuk a_n adalah

    \[ a_{n} = A_{1}1^{n}+A_{2}4^{n} \]

Dengan mensubstitusi nilai awal akan dihasilkan

    \begin{equation*} \begin{split} 1 = a_{0} &= A_{1}+A_{2}\\ 7= a_{1}&=A_{1}+4A_{2}. \end{split} \end{equation*}

Diperoleh

    \begin{equation*} A_{1}=-1~\text{dan}~A_{2}=2. \end{equation*}

Jadi a_{n}=(-1)\cdot1^{n}+2\cdot 4^{n}=2\cdot 4^{n}-1 untuk setiap n\geq 0.

Credit: Iwan Ernanto

Pembahasan Soal 2 Relasi Rekurensi

Tutorial Senin, 23 Agustus 2021

Soal Diambil barisan Fibonacci \{ F_{n} \} = 0,1, 1, 2, 3, 5, 8, 13, \ldots. Tentukan formula untuk F_n!

Pembahasan

Perhatikan bahwa relasi rekurensi yang dipenuhi adalah F_{n + 2} = F_{n + 1} + F_{n}. Selanjutnya dapat dicek juga persamaan polinomial yang dipenuhi adalah

    \[ x^{2} - x - 1 .\]

Jadi ketika dihitung akar-akar karakteristiknya akan menghasilkan

    \[ r_{1}, r_{2} = \frac{1 \pm \sqrt{1 - 4(-1)}}{2} = \frac{1}{2} \pm\frac{\sqrt{5}}{2} .\]

Jadi k = 2 dengan m_{1} = 1 = m_{2}. Jika dikembalikan ke rumus umumnya menghasilkan

    \[ F_{n} = A_{1}r_{1}^{n} + A_{2}r_{2}^{n} = A_{1}\left(\frac{1}{2} - \frac{\sqrt{5}}{2}\right)^{n} + A_{2}\left(\frac{1}{2} +\frac{\sqrt{5}}{2}\right)^{n} .\]

Selanjutnya nilai awal disubstitusikan ke persamaan di atas, menghasilkan:

    \begin{eqnarray*} 0 = F(0) & = & A_{1}\left(\frac{1}{2} - \frac{\sqrt{5}}{2}\right)^{0} + A_{2}\left(\frac{1}{2} +\frac{\sqrt{5}}{2}\right)^{0}\\ 1 = F(1) & = & A_{1}\left(\frac{1}{2} - \frac{\sqrt{5}}{2}\right) + A_{2}\left(\frac{1}{2} +\frac{\sqrt{5}}{2}\right) \end{eqnarray*} read more

Pembahasan Soal 1 Relasi Rekurensi

Tutorial Senin, 23 Agustus 2021

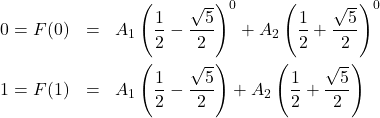
Soal: Diberikan barisan \{a_{n}\} dengan relasi rekurensi a_{n + 1} = 2a_{n} dan a_{0} = 1. Carilah formula dari a_n!

Pembahasan:

Persamaan karakteristik p(x) = x - 2. Diperoleh k = 1, m_{1} = 1, dan r_{1} = 2. Jadi,

    \[ a_{n} = A_{1}2^{n} .\]

Dari nilai awal ketika disubstitusi diperoleh

    \[ n = 0 \mapsto 1 = a_{0} = A_{1}2^{0} \Longrightarrow A_{1} = 1 .\]

Hal ini mengakibatkan formula untuk a_n adalah

    \[ a_{n} = 1\cdot 2^{n} = 2^{n} \]

Credit: Iwan Ernanto

Virtual Tour FMIPA UGM

Artikel Minggu, 22 Agustus 2021

Fakultas yang mengasuh Matematika dan Ilmu Pengetahuan Alam di Universitas Gadjah Mada diresmikan berdirinya pada tanggal 19 September 1955 dengan Surat Keputusan Menteri Pendidikan, Pengajaran dan Kebudayaan tanggal 15 September 1955 nomor 53759/Kab. Saat ini kampus FMIPA dijadikan satu yang berada di Sekip Utara Bulaksumur Yogyakarta. Di video ini kita akan diajak oleh salah satu mahasiswa matematika, yaitu Silvina Rosita Yulianti untuk keliling FMIPA UGM.

Pembahasan Soal 5 Prinsip Sarang Merpati

Tutorial Minggu, 22 Agustus 2021

Soal: Diketahui A=\{1,2,3,4,5,6\}. Untuk masing-masing i=1,2,\ldots,2021,

    \[f_{i} : A \rightarrow A\]

fungsi bijektif. Apakah benar terdapat 1\leq i<j<k\leq 2021 yang memenuhi f_{i}=f_{j}=f_{k}? Jelaskan!

Pembahasan:

Diketahui A=\{1,2,3,4,5,6\}. Untuk masing-masing i=1,2,\ldots,2021,

    \[f_{i} : A \rightarrow A\]

fungsi bijektif.

Karena f_{i} : A \rightarrow A fungsi bijektif, maka ada sebanyak 6!=720 kemungkinan pemetaan yang berbeda dari domain ke kodomain. Andaikan terdapat i,j,k sedemikian sehingga 1\leq i<j<k\leq 2021. Maka banyaknya fungsi pemetaan yang akan memetakan ke tempat yang sama ada sebanyak 2\times 6! + 1 = 1441. Dengan menggunakan prinsip sarang burung ada setidaknya \lceil \frac{1441}{720}\rceil=3 fungsi yang melakukan pemetaan yang sama. read more

Pembahasan Soal 4 Prinsip Sarang Merpati

Tutorial Minggu, 22 Agustus 2021

Soal: Diberikan himpunan

    \[\displaystyle A = \Big\{a_{n}|a_{n} = \binom{2021}{n},n=0,1,2,\ldots,1010\Big\}.\]

Buktikkan bahwa ada sedikitnya 253 anggota A yang mempunyai sisa yang sama ketika dibagi 4.

Pembahasan:

Misal A_{i} adalah himpunan yang berisikan bilangan yang bersisa i jika dibagi 4, dengan A_{i} \subseteq A, \forall i = 0,1,2,3.
Katakan A sebagai kumpulan merpati dengan |A|=1010 dan A_{i} sebagai sangkar. Maka berdasarkan prinsip sarang burung, satu sangkar paling sedikit berisi \lceil \frac{1010}{4}\rceil = 253 merpati.

Jadi, terbukti bahwa setidaknya ada 253 anggota A yang mempunyai sisa yang sama ketika dibagi 4. read more

Pembahasan Soal 3 Prinsip Sarang Merpati

Tutorial Minggu, 22 Agustus 2021

Soal: Diberikan himpunan A \subset \{ 1,2,3,4,5,6,7,8,9\} dengan 1\in A dan |A| = 5
1. Buktikkan bahwa pasti ada dua anggota (berbeda) dari A yang jumlahnya habis dibagi 2;
2. Buktikkan bahwa pasti ada dua anggota (berbeda) dari A yang jumlahnya habis dibagi 3;
3. Selidiki apakah pasti ada dua anggota (berbeda) dari A yang jumlahnya habis dibagi 6. Jika tidak, berikan penyangkalnya;
4. Jika diberikan himpunan B \subseteq \{1,2,3,4,5,6,7,8,9\} dengan 1\in B dan |B| = n. Tentukan bilangan terkecil n sehingga pasti ada dua anggota (berbeda) dari B yang jumlahnya habis dibagi 6. read more