Arsip 2021:

22 Agustus

Virtual Tour FMIPA UGM

Artikel Minggu, 22 Agustus 2021

Fakultas yang mengasuh Matematika dan Ilmu Pengetahuan Alam di Universitas Gadjah Mada diresmikan berdirinya pada tanggal 19 September 1955 dengan Surat Keputusan Menteri Pendidikan, Pengajaran dan Kebudayaan tanggal 15 September 1955 nomor 53759/Kab. Saat ini kampus FMIPA dijadikan satu yang berada di Sekip Utara Bulaksumur Yogyakarta. Di video ini kita akan diajak oleh salah satu mahasiswa matematika, yaitu Silvina Rosita Yulianti untuk keliling FMIPA UGM.

Pembahasan Soal 5 Prinsip Sarang Merpati

Tutorial Minggu, 22 Agustus 2021

Soal: Diketahui A=\{1,2,3,4,5,6\}. Untuk masing-masing i=1,2,\ldots,2021,

    \[f_{i} : A \rightarrow A\]

fungsi bijektif. Apakah benar terdapat 1\leq i<j<k\leq 2021 yang memenuhi f_{i}=f_{j}=f_{k}? Jelaskan!

Pembahasan:

Diketahui A=\{1,2,3,4,5,6\}. Untuk masing-masing i=1,2,\ldots,2021,

    \[f_{i} : A \rightarrow A\]

fungsi bijektif.

Karena f_{i} : A \rightarrow A fungsi bijektif, maka ada sebanyak 6!=720 kemungkinan pemetaan yang berbeda dari domain ke kodomain. Andaikan terdapat i,j,k sedemikian sehingga 1\leq i<j<k\leq 2021. Maka banyaknya fungsi pemetaan yang akan memetakan ke tempat yang sama ada sebanyak 2\times 6! + 1 = 1441. Dengan menggunakan prinsip sarang burung ada setidaknya \lceil \frac{1441}{720}\rceil=3 fungsi yang melakukan pemetaan yang sama. read more

Pembahasan Soal 4 Prinsip Sarang Merpati

Tutorial Minggu, 22 Agustus 2021

Soal: Diberikan himpunan

    \[\displaystyle A = \Big\{a_{n}|a_{n} = \binom{2021}{n},n=0,1,2,\ldots,1010\Big\}.\]

Buktikkan bahwa ada sedikitnya 253 anggota A yang mempunyai sisa yang sama ketika dibagi 4.

Pembahasan:

Misal A_{i} adalah himpunan yang berisikan bilangan yang bersisa i jika dibagi 4, dengan A_{i} \subseteq A, \forall i = 0,1,2,3.
Katakan A sebagai kumpulan merpati dengan |A|=1010 dan A_{i} sebagai sangkar. Maka berdasarkan prinsip sarang burung, satu sangkar paling sedikit berisi \lceil \frac{1010}{4}\rceil = 253 merpati.

Jadi, terbukti bahwa setidaknya ada 253 anggota A yang mempunyai sisa yang sama ketika dibagi 4. read more

Pembahasan Soal 3 Prinsip Sarang Merpati

Tutorial Minggu, 22 Agustus 2021

Soal: Diberikan himpunan A \subset \{ 1,2,3,4,5,6,7,8,9\} dengan 1\in A dan |A| = 5
1. Buktikkan bahwa pasti ada dua anggota (berbeda) dari A yang jumlahnya habis dibagi 2;
2. Buktikkan bahwa pasti ada dua anggota (berbeda) dari A yang jumlahnya habis dibagi 3;
3. Selidiki apakah pasti ada dua anggota (berbeda) dari A yang jumlahnya habis dibagi 6. Jika tidak, berikan penyangkalnya;
4. Jika diberikan himpunan B \subseteq \{1,2,3,4,5,6,7,8,9\} dengan 1\in B dan |B| = n. Tentukan bilangan terkecil n sehingga pasti ada dua anggota (berbeda) dari B yang jumlahnya habis dibagi 6. read more

Pembahasan Soal 2 Prinsip Sarang Merpati

Tutorial Minggu, 22 Agustus 2021

Soal: Diberikan himpunan A yang terdiri atas 20 bilangan yang diambil dari himpunan S=\{1,4,7,\ldots,100\}. Buktikkan bahwa setidaknya ada 2 bilangan yang dipilih dari A berjumlah 104.

Pembahasan:

Dengan melihat pola dari himpunan S, jelas bahwa S membentuk barisan a_{n}=3n-2,\forall n \in \{1,2,3,\ldots,34\}. Jika a_{i} dan a_{j} adalah dua buah bilangan yang dipilih dari S yang memiliki jumlah 104, maka diperoleh

    \[3i-2+3j-2=140 \iff i+j=36 .\]

Artinya, pernyataan pada soal akan ekuivalen dengan menunjukkan terdapat 20 bilangan yang dipilih dari \{1,2,3,\ldots,34\} maka ada 2 bilangan yang jumlahnya 36. read more

Pembahasan Soal 1 Prinsip Sarang Merpati

Tutorial Minggu, 22 Agustus 2021

Soal: Terdapat 51 bilangan yang dipilih dari bilangan bulat antara 1 dan 100 secara inklusif. Buktikkan bahwa terdapat 2 bilangan yang dipilih adalah berurutan.

Pembahasan:

Dari 100 bilangan tersebut, akan dibagi menjadi 50 partisi, yaitu \{1, 2\}, \{3, 4\},\ldots,\{99, 100\} sebagai sarang merpati. Selanjutnya, dipilih 51 bilangan sebagai merpati. Dengan menggunakan prinsip sangkar burung, maka terdapat \lceil \frac{51}{50} \rceil =2 bilangan yang berurutan.

Terbukti bahwa jika 51 bilangan yang dipilih dari bilangan bulat antara 1 dan 100 secara inklusif, maka terdapat 2 bilangan dari bilangan bulat yang dipilih adalah berurutan. read more

Pembahasan Soal 4 Prinsip Inklusi-Eksklusi

Tutorial Minggu, 22 Agustus 2021

File Tayangan

Soal: 

Tentukan banyaknya permutasi dari himpunan \{1, 2,\ldots, 9\} dimana paling tidak terdapat satu bilangan ganjil yang berada pada urutan aslinya.

Contoh : angka 1 diletakan pada urutan pertama, angka 2 diletakan pada urutan kedua.

Pembahasan:

Petama-tama, dipilih satu bilangan ganjil dan diletakan kedalam urutan aslinya, diperoleh banyaknya cara yaitu \binom{5}{1} = 5 cara dan permutasikan terhadap 8 bilangan lainnya, diperoleh 8! cara, dengan prinsip permutasi perkalian didapat total caranya yaitu 5\times 8!. Dipilih dua bilangan ganjil dan diletakan kedalam urutan aslinya, diperoleh banyaknya cara yaitu \binom{5}{2} = 10 cara dan permutasikan terhadap 7 bilangan lainnya, diperoleh 7! cara, dengan prinsip permutasi perkalian didapat total caranya yaitu 10\times7!.
Selanjutnya, dipilih tiga bilangan ganjil dan diletakan kedalam urutan aslinya, diperoleh banyaknya cara yaitu \binom{5}{3} = 10 cara dan permutasikan terhadap 6 bilangan lainnya, diperoleh 7! cara, dengan prinsip permutasi perkalian didapat total caranya yaitu 10\times 6!. Dipilih empat bilangan ganjil dan diletakan kedalam urutan aslinya, diperoleh banyaknya cara yaitu \binom{5}{4} = 5 cara dan permutasikan terhadap 5 bilangan lainnya, diperoleh 5! cara, dengan prinsip permutasi perkalian didapat total caranya yaitu 5\times 5!. Dipilih lima bilangan ganjil dan diletakan kedalam urutan aslinya, diperoleh banyaknya cara yaitu \binom{5}{5} = 1 cara dan permutasikan terhadap 4 bilangan lainnya, diperoleh 4! cara, dengan prinsip permutasi perkalian didapat total caranya yaitu 1\times4!. read more

Pembahasan Soal 3 Prinsip Inklusi-Eksklusi

Tutorial Minggu, 22 Agustus 2021

File Tayangan

Soal: A bakery sells chocolate, cinnamon, and plain doughnuts and at a particular time has 6 chocolate, 6 cinnamon, and 3 plain. If a box contains 12 doughnuts, how many different option are there for a box of doughnuts?

Pembahasan:

Dari informasi pada soal, didapat multiset T=\{6\cdot x,\cdot y,3\cdot z \}, dengan x adalah coklat, y adalah cinnamon, z plain. Akan dicari banyaknya solusi dari

    \[x+y+z=12\]

dengan x\leq6,y\leq6,z\leq3 .
Dinotasikan

    \begin{align*} \begin{cases} A = \{x\in\mathbb{Z}|x+y+z=12,x\geq 7\} \\ B = \{ y\in\mathbb{Z}|x+y+z=12, y\geq 7\} \\ C = \{z\in\mathbb{Z}|x+y+z=12,z\geq 4\} \\ \end{cases} \end{align*}

Untuk x,y,z \geq 0, menurut Stars and Bars theorem, diperoleh banyaknya solusi, yaitu

    \[|S| =\binom{3+12-1}{12} = \binom{14}{12} = 91 .\]

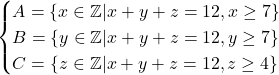
Untuk memperoleh himpunan x \leq 6, y \leq 6, z \leq 3, yaitu irisan dari negasi ketiga himpunan tersebut. Dinotasikan read more

Pembahasan Soal 2 Prinsip Inklusi-Eksklusi

Tutorial Minggu, 22 Agustus 2021

File Tayangan

Soal: Tentukan banyaknya bilangan dari 1 sampai 70 yang relatif prima terhadap 70.

Pembahasan:

Diketahui bahwa pembagi prima dari 70 yaitu 2,5, dan 7. Selanjutnya, di defenisikan A adalah himpunan bilangan bulat yang habis dibagi 2, B adalah himpunan bilangan bulat yang habis dibagi 5, A adalah himpunan bilangan bulat yang habis dibagi 7. Akan dicari banyaknya bilangan dari 1 sampai 70 yang relatif prima terhadap 70 yaitu |A^{c}\cup B^{c} C^{c}|.

Diperoleh, read more

Pembahasan Soal 1 Prinsip Inklusi-Eksklusi

Tutorial Minggu, 22 Agustus 2021

File Tayangan

Soal: Tentukan banyaknya bilangan bulat dari 1 hingga 2021 yang tidak habis dibagi 4,6, dan 9.

Pembahasan:

Dinotasikan himpunan :

    \begin{align*} \begin{cases} A &= \{x\in\mathbb{Z}\mid 1 \leq x \leq 2021, \textit{x} \ \text{habis dibagi} \ 4 \} \\ B &= \{x\in\mathbb{Z}\mid 1 \leq x \leq 2021, \textit{x} \ \text{habis dibagi} \ 6\} \\ C &= \{x\in\mathbb{Z}\mid 1 \leq x \leq 2021, \textit{x} \ \text{habis dibagi} \ 9\} \end{cases} \end{align*}

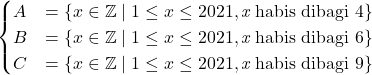
Akan ditentukan banyaknya bilangan bulat antara 1 dan 2021 yang tidak habis dibagi 4,6, dan 9, yaitu |A^{c} \cup B^{c} \cup C^{c}|.
Diperoleh,

    \begin{align*} |A| &= \lfloor\frac{2021}{4}\rfloor =505 & |B| &= \lfloor\frac{2021}{6}\rfloor = 336\\ |C| &= \lfloor\frac{2021}{9}\rfloor = 224 & |A\cap B| &= \lfloor\frac{2021}{12}\rfloor = 168 \\ |B\cap C| &= \lfloor\frac{2021}{18}\rfloor = 224 & |A\cap C| &= \lfloor\frac{2021}{36}\rfloor = 56 \\ |A\cap B \cap C| &= \lfloor\frac{2021}{36}\rfloor = 56 & |S| = 2019 \end{align*}

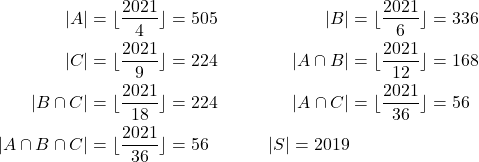
Dengan menggunakan Prinsip Inklusi-Eksklusi, diperoleh

    \begin{align*} |A^{c} \cup B^{c} \cup C^{c}| &= |S| - \Bigg(|A|+|B|+|C|-\Big(|A\cap B|+|A\cap C|+|B \cap C|\Big)+|A\cap B \cap C|\Bigg) \\ &= 1234. \end{align*}

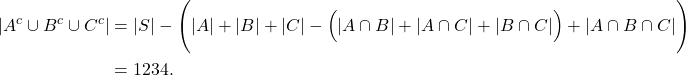
Credit: Fadhlan Zhaahiran