Pembahasan Soal 1 Induksi Matematika

Tutorial
22 Agustus 2021, 07.44
Oleh: isnainiuha
0

Soal: Buktikan melalui induksi matematika, untuk setiap bilangan bulat $n\geq 1$ berlaku $\left(n!\leq n^{n}\right)$ .

Pembahasan:

Pertama-tama akan ditunjukkan benar untuk $n=1$ .

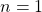Diperoleh

$1!=1 \leq 1^1 .$

Jadi, untuk $n=1$ terbukti benar bahwa $n^{n}\leq n!.$

Diasumsikan benar untuk 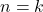$n=k$ , berlaku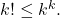 $k!\leq k^{k}.$
Akan ditunjukkan jika 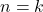$n=k$ benar, maka 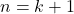$n=k+1$ benar.
Diperoleh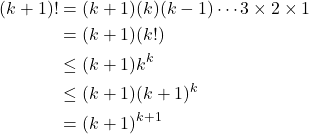

$\begin{align*} (k+1)! &= (k+1)(k)(k-1)\cdots 3 \times 2 \times 1 \\ &= (k+1)(k!) \\ &\leq (k+1) k^{k} \\ &\leq (k+1) (k+1)^{k} \\ &= (k+1)^{k+1} \end{align*}$

Dengan induksi matematika, terbukti bahwa untuk 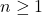$n\geq 1$ berlaku $n!\leq n^{n}$ .

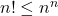Credit: Fadhlan Zhaahiran

Leave A Comment Batalkan balasan