Pembahasan Soal 3 Induksi Matematika

Soal: Buktikan dengan induksi bahwa untuk setiap $n \in \mathbb{Z^{+}},$ $3\mid 5^{n}+ 2\times 11^{n}.$

Pembahasan:

Dinotasikan $S(n)=5^{n}+ 2 \times 11^{n}.$

Pertama-tama akan ditunjukkan 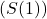$(S(1))$ benar. Diperhatikan bahwa
$5^{1}+2\times11^{1}=5+22=27=3^{3} .$

Jadi, pernyataan 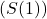$(S(1))$ benar.
Diasumsikan 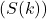$(S(k))$ benar. Diperoleh 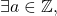$\exists a \in \mathbb{Z},$ sedemikian sehingga
$5^{k}+2\times11^{k}=3a .$
Akan ditunjukkan jika 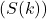$(S(k))$ benar, maka 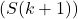$(S(k+1))$ juga benar.
Diperhatikan bahwa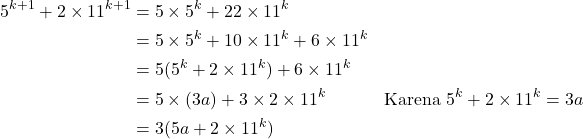

$\begin{align*} 5^{k+1}+2\times11^{k+1} &= 5 \times 5^{k}+ 22 \times11^{k} \\ &= 5\times5^{k} + 10\times11^{k} + 6\times11^{k} \\ &= 5 ( 5^{k} + 2\times 11^{k}) + 6\times11^{k} \\ &= 5 \times(3a) + 3 \times 2 \times 11^{k} && \text{Karena}\ 5^{k}+2\times11^{k}=3a \\ &= 3 (5a+ 2\times11^{k}) \end{align*}$

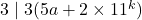Karena $3\mid 3 (5a+ 2\times11^{k})$ , maka pernyataan 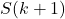$S(k+1)$ benar.

Dengan induksi matematika, $(S(n))$ terbukti benar untuk setiap $n \in \mathbb{Z^{+}}.$

Credit: Fadhlan Zhaahiran

Kalender