Soal: Tentukan banyaknya solusi bulat non negatif dari
![]()
dengan kendala ![]()
![]()
![]()
Pembahasan:
Untuk ![]() menurut Stars and Bars theorem, diperoleh banyaknya solusi, yaitu
menurut Stars and Bars theorem, diperoleh banyaknya solusi, yaitu
![]()
Didefinisikan
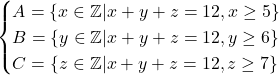
Untuk memperoleh himpunan ![]()
![]()
![]() yaitu irisan dari negasi ketiga himpunan tersebut. Dinotasikan
yaitu irisan dari negasi ketiga himpunan tersebut. Dinotasikan
![]()
Dengan Prinsip Inklusi-Eksklusi, akan ditentukan banyak solusinya dari ![]()
Diperoleh,
![]()
Selanjutnya, akan dicari:
- Solusi
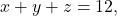 dengan kendala
dengan kendala
![Rendered by QuickLaTeX.com \[\begin{array}{cc} x \geq 5 \\ (x-5) \geq 0 \\ x_1 \geq 0, \text{untuk} \ x_1 = x-5 \end{array}\]](https://matematikadiskrit.mipa.ugm.ac.id/wp-content/ql-cache/quicklatex.com-e2d40a967329d01c5c80ffccb908fad8_l3.png)
Maka,
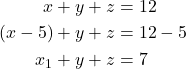
Untuk
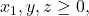 menurut Stars and Bars Theorem, diperoleh banyaknya solusi yaitu
menurut Stars and Bars Theorem, diperoleh banyaknya solusi yaitu![Rendered by QuickLaTeX.com \[|A| = \binom{7+3-1}{7} = \binom{9}{7} = 36.\]](https://matematikadiskrit.mipa.ugm.ac.id/wp-content/ql-cache/quicklatex.com-5fe1835bc7e8e95f56d24c1149927ffd_l3.png)
- Solusi
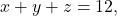 dengan kendala
dengan kendala
![Rendered by QuickLaTeX.com \[\begin{array}{cc} y \geq 6 \\ (y-6) \geq 0 \\ y_1 \geq 0, \text{untuk} \ y_1 = y-6 \end{array}\]](https://matematikadiskrit.mipa.ugm.ac.id/wp-content/ql-cache/quicklatex.com-9eac1c3825ff2d925012f778834d7a10_l3.png)
Maka,
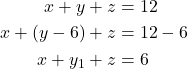
Untuk
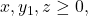 menurut Stars and Bars Theorem, diperoleh banyaknya solusi yaitu
menurut Stars and Bars Theorem, diperoleh banyaknya solusi yaitu![Rendered by QuickLaTeX.com \[|B| = \binom{6+3-1}{6} = \binom{8}{6} = 28.\]](https://matematikadiskrit.mipa.ugm.ac.id/wp-content/ql-cache/quicklatex.com-15803e2aa95af4159b08d49bbca763c7_l3.png)
- Solusi
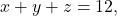 dengan kendala
dengan kendala
![Rendered by QuickLaTeX.com \[\begin{array}{cc} z \geq 7 \\ (z-7) \geq 0 \\ z_1 \geq 0, \text{untuk} \ z_1 = z-7 \end{array}\]](https://matematikadiskrit.mipa.ugm.ac.id/wp-content/ql-cache/quicklatex.com-911df209c4f2e91929278ca977fb95ac_l3.png)
Maka,
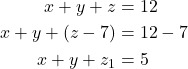
Untuk
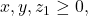 menurut Stars and Bars Theorem, diperoleh banyaknya solusi yaitu
menurut Stars and Bars Theorem, diperoleh banyaknya solusi yaitu![Rendered by QuickLaTeX.com \[|C| = \binom{5+3-1}{5} = \binom{7}{5} = 21.\]](https://matematikadiskrit.mipa.ugm.ac.id/wp-content/ql-cache/quicklatex.com-442452c0cfa7b7d9736400b7f6f15a18_l3.png)
- Solusi
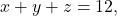 dengan kendala
dengan kendala
![Rendered by QuickLaTeX.com \[\begin{array}{cc} x \geq 5, y \geq 6 \\ (x-5) \geq 0, (y-6) \geq 0 \\ x_1 \geq 0,y_1 \geq 0, \text{untuk} \ x_1 = x-5 , y_1 = x-6 \end{array}\]](https://matematikadiskrit.mipa.ugm.ac.id/wp-content/ql-cache/quicklatex.com-e684649a2a87f5f0c29a3101a6aae14f_l3.png)
Maka,
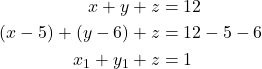
Untuk
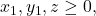 menurut Stars and Bars Theorem, diperoleh banyaknya solusi yaitu
menurut Stars and Bars Theorem, diperoleh banyaknya solusi yaitu![Rendered by QuickLaTeX.com \[|A \cap B| = \binom{1+3-1}{1} = \binom{3}{1} = 3.\]](https://matematikadiskrit.mipa.ugm.ac.id/wp-content/ql-cache/quicklatex.com-1b20901066da8bd36e453628e90cdf25_l3.png)
- Solusi
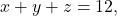 dengan kendala
dengan kendala
![Rendered by QuickLaTeX.com \[\begin{array}{cc} x \geq 5, z \geq 7 \\ (x-5) \geq 0, (z-7) \geq 0 \\ x_1 \geq 0,z_1 \geq 0, \text{untuk} \ x_1 = x-5 , z_1 = z-7 \end{array}\]](https://matematikadiskrit.mipa.ugm.ac.id/wp-content/ql-cache/quicklatex.com-d0fb5a7b86c0482934a237ea2a406f20_l3.png)
Maka,
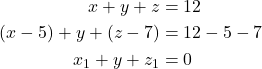
Untuk
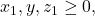 menurut Stars and Bars Theorem, diperoleh banyaknya solusi yaitu
menurut Stars and Bars Theorem, diperoleh banyaknya solusi yaitu![Rendered by QuickLaTeX.com \[|A \cap C| = \binom{0+3-1}{0} = \binom{2}{0} = 1.\]](https://matematikadiskrit.mipa.ugm.ac.id/wp-content/ql-cache/quicklatex.com-458a6917c2919757caf43c6bde067cc6_l3.png)
- Solusi
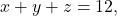 dengan kendala
dengan kendala
![Rendered by QuickLaTeX.com \[\begin{array}{cc} y \geq 6, z \geq 7 \\ (y-6) \geq 0, (z-7) \geq 0 \\ y_1 \geq 0,z_1 \geq 0, \text{untuk} \ y_1 = y-6 , z_1 = z-7 \end{array}\]](https://matematikadiskrit.mipa.ugm.ac.id/wp-content/ql-cache/quicklatex.com-6c55ebee7755bb36acf8163d8804e04d_l3.png)
Maka,
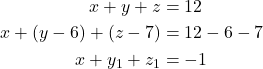
Diperhatikan bahwa,
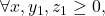 berlaku
berlaku 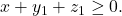 Sedangkan, pernyataan awal akan ditentukan banyaknya solusi
Sedangkan, pernyataan awal akan ditentukan banyaknya solusi 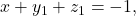 dengan
dengan 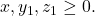 Akibatnya, diperoleh
Akibatnya, diperoleh 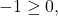 kontradiksi dengan pernyataan awal dimana
kontradiksi dengan pernyataan awal dimana 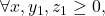 berlaku
berlaku 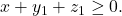 Dengan demikian, banyaknya solusi
Dengan demikian, banyaknya solusi
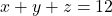 dengan kendala
dengan kendala 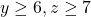 yaitu
yaitu![Rendered by QuickLaTeX.com \[|B \cap C |=0.\]](https://matematikadiskrit.mipa.ugm.ac.id/wp-content/ql-cache/quicklatex.com-07e80b9fd13368af990518534cf5910c_l3.png)
- Solusi
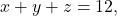 dengan kendala
dengan kendala
![Rendered by QuickLaTeX.com \[\begin{array}{cc} x\geq 5, y \geq 6, z \geq 7 \\ (x-5)\geq 0, (y-6) \geq 0, (z-7) \geq 0 \\ x_1\geq 0, y_1 \geq 0,z_1 \geq 0, \text{ untuk } \ x_1 = x - 5, y_1 = y-6 , z_1 = z-7 \end{array}\]](https://matematikadiskrit.mipa.ugm.ac.id/wp-content/ql-cache/quicklatex.com-fda326711c5b241ba6294f86b4510e4d_l3.png)
Maka,
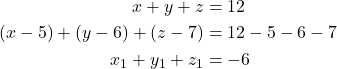
Diperhatikan bahwa,
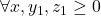 berlaku
berlaku 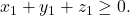 Sedangkan, pernyataan awal akan ditentukan banyaknya solusi
Sedangkan, pernyataan awal akan ditentukan banyaknya solusi 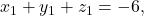 dengan
dengan 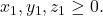
Akibatnya, diperoleh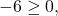 kontradiksi dengan pernyataan awal dimana
kontradiksi dengan pernyataan awal dimana 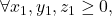 berlaku
berlaku 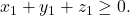
Dengan demikian, banyaknya penyelesaian
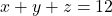 dengan kendala
dengan kendala 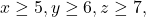 yaitu
yaitu![Rendered by QuickLaTeX.com \[|A \cap B \cap C|=0.\]](https://matematikadiskrit.mipa.ugm.ac.id/wp-content/ql-cache/quicklatex.com-ca1048cff73679cb2adb5e2ccf5d0bf8_l3.png)
Dengan menggunakan Prinsip Inklusi-Eksklusi, diperoleh
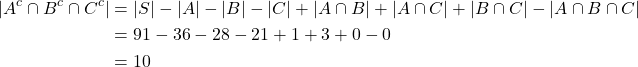
Maka, banyaknya solusi dari ![]() dengan kendala
dengan kendala ![]()
![]()
![]() yaitu sebanyak 10 solusi unik.
yaitu sebanyak 10 solusi unik.
Jika menghimpun secara manual untuk penyelesaian persamaan
![]()
yang memenuhi kendala
![]()
![]() dan
dan ![]()
Diperoleh himpunan penyelesaian nya sebagai berikut :
![]()
Jadi diperoleh ada 10 solusi unik.
Credit: Fadhlan Zhaahiran
