
Soal: Diberikan barisan ![]() dikatakan barisan Fibonnachi di mana barisan bilangan yang dihasilkan dari penjumlahan dua bilangan sebelumnya, yang memenuhi
dikatakan barisan Fibonnachi di mana barisan bilangan yang dihasilkan dari penjumlahan dua bilangan sebelumnya, yang memenuhi ![]() untuk
untuk ![]() . Buktikkan dengan induksi matematika bahwa untuk setiap
. Buktikkan dengan induksi matematika bahwa untuk setiap ![]() , berlaku
, berlaku
![]()
Pembahasan:
- Akan dibuktikkan benar untuk
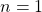 dan
dan 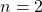 , diperoleh
, diperoleh
![Rendered by QuickLaTeX.com \[a_{1} = 1 = \frac{1+1}{2} < \frac{1+\sqrt{5}}{2} = \Big(\frac{1+\sqrt{5}}{2}\Big)^{1} .\]](https://matematikadiskrit.mipa.ugm.ac.id/wp-content/ql-cache/quicklatex.com-22dcd3b3c1bdfac1a1fe2272efe937d4_l3.png)
![Rendered by QuickLaTeX.com \[a_{2} = 2 = \frac{6+2}{4} < \frac{6+2\sqrt{5}}{6} = \Big(\frac{1+\sqrt{5}}{2}\Big)^{2} .\]](https://matematikadiskrit.mipa.ugm.ac.id/wp-content/ql-cache/quicklatex.com-32f5a82f4e5042bfb6ca44656f282147_l3.png)
Jadi, terbukti benar untuk
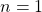 dan
dan 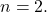
- Diasumsikan benar untuk
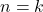 , berlaku
, berlaku
![Rendered by QuickLaTeX.com \[a_{k}<\Big(\frac{1+\sqrt{5}}{2}\Big)^{k} .\]](https://matematikadiskrit.mipa.ugm.ac.id/wp-content/ql-cache/quicklatex.com-18e9aba6e63e584dae7f78d55bc4a049_l3.png)
- Untuk
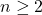 , diasumsikan
, diasumsikan 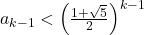 . Akan dibuktikkan benar untuk
. Akan dibuktikkan benar untuk 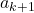 , diperoleh
, diperoleh
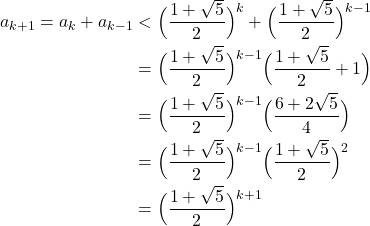
Jadi, terbukti benar untuk ![]() . Dengan demikian dengan induksi terbukti bahwa untuk setiap
. Dengan demikian dengan induksi terbukti bahwa untuk setiap ![]() , berlaku
, berlaku ![]()
Credit: Fadhlan Zhaahiran
