
Soal: Formulasikan dan buktikan dengan induksi rumus umum dari bentuk berikut
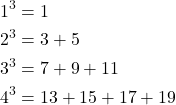
Pembahasan:
Diperhatikan bahwa pada soal akan memiliki bentuk umum
![]()
Akan dibuktikan dengan induksi matematika bahwa ![]() di atas benar untuk setiap
di atas benar untuk setiap ![]()
- Untuk
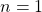 maka
maka
![Rendered by QuickLaTeX.com \[p(1) : 1^3 = 1 = 1^2 - 1 - 1 + 2\]](https://matematikadiskrit.mipa.ugm.ac.id/wp-content/ql-cache/quicklatex.com-0948060cfe0d889debee157c7aaf58a9_l3.png)
sehingga p(1) benar.
- Asumsikan bahwa
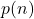 benar. Artinya berlaku
benar. Artinya berlaku
![Rendered by QuickLaTeX.com \[p(n) : n^3 = \sum_{i=1} ^n (n^2 -n-1 + 2i) .\]](https://matematikadiskrit.mipa.ugm.ac.id/wp-content/ql-cache/quicklatex.com-c0d7e05ffdfb713ce5bbbaba6d916273_l3.png)
Akan dibuktikan bahwa
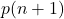 benar. Mudah dilihat bahwa
benar. Mudah dilihat bahwa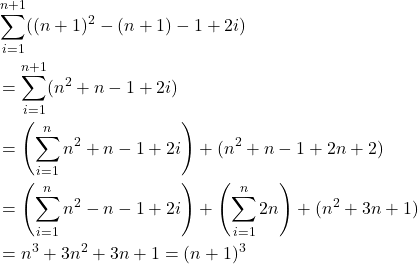
Terbukti benar untuk
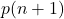 .
.
Terbukti bentuk pada soal memiliki formula umum ![]()
Credit: Naelufa Syifna W M
