Pembahasan Soal 6 Relasi Rekurensi

Soal Solve the recurrence relation

    \[a_{n}=3a_{n-1}-2a_{n-2}+4n\cdot 3^{n},\]

with initial conditions a_{0} = -44, a_{1} = -78.

Pembahasan

Diberikan relasi rekurensi

    \[a_{n}=3a_{n-1}-2a_{n-2}+4n\cdot 3^{n},\]

dengan nilai awal a_{0} = -44, a_{1} = -78.
Diperhatikan bahwa polinomial karakteristik rekurensi linear homogen yang berkorespondensi dengan relasi rekurensi tersebut adalah

    \[p(x)=x^{2}-3x+2=(x-1)(x-2)\]

dengan akar-akarnya adalah 1 dan 2. Dengan demikian solusi homogennya mempunyai bentuk

    \[a_{n}^{(h)}=A+B2^{n}\]

untuk suatu bilangan real A dan B.

Selanjutnya, mengingat f(n)=4n\cdot 3^{n} dan 3 bukan akar dari polinomial karakteristik p(x), maka solusi parsialnya mmiliki bentuk

    \[a_{n}^{(p)}=(Cn+D)3^{n}\]

untuk suatu bilangan real C dan D.

Diperhatikan bahwa solusi parsial tersebut memenuhi relasi rekurensi, jadi

    \begin{equation*} \begin{split} a_{n}^{(p)}&=3a_{n-1}^{(p)}-2a_{n-2}^{(p)}+4n\cdot 3^{n}\\ (Cn+D)3^{n}&=3(C(n-1)+D)3^{n-1}-2(C(n-2)+D)3^{n-2}+4n\cdot 3^{n}\\ 9(Cn+D)&=9(C(n-1)+D)-2(C(n-2)+D)+36n\\ 9Cn+9D&=(9C-2C+36)n+(-9C+9D+4C-2D) \end{split} \end{equation*}

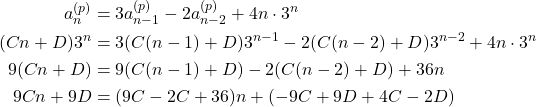
Sehingga diperoleh sistem persamaan linear berikut:

    \begin{equation*} \begin{split} 7C+36&= 9C \iff C=18\\ -5C+7D&=9D \iff D=\displaystyle \frac{-5}{2}C=-45 \end{split} \end{equation*}

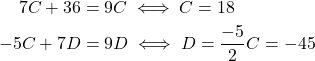
Dengan demikian solusi parsial dari relasi rekurensi

    \[a_{n}=3a_{n-1}-2a_{n-2}+4n\cdot 3^{n}\]

adalah

    \[a_{n}^{(p)}=(18n-45)3^{n}.\]

Selanjutnya, dieprhatikan bahwa solusi umum dari relasi rekurensi mempunyai bentuk

    \[a_{n}=a_{n}^{(h)}+a_{n}^{(p)}=A+B2^{n}+(18n-45)3^{n}.\]

Mengingat nilai awal a_{0} = -44, a_{1} = -78, maka diperoleh

    \begin{equation*} \begin{split} -44&=A+B-45 \iff A+B=1\\ -78&=A+2B-81\iff A+2B=3 \end{split} \end{equation*}

dan berakibat A=-1 dan B=2.

Kesimpulan: Solusi dari relasi rekurensi relasi rekurensi

    \[a_{n}=3a_{n-1}-2a_{n-2}+4n\cdot 3^{n},\]

dengan nilai awal a_{0} = -44, a_{1} = -78 adalah

    \[a_{n}=-1+2\cdot2^{n}+(18n-45)3^{n}\]

untuk setiap n\geq 0

 

Credit: Iwan Ernanto

 

Video Penjelasan:

Leave A Comment

Alamat email Anda tidak akan dipublikasikan.

*