
Soal
Tentukan bentuk umum dari barisan Fibonacci.
Pembahasan
Barisan Fibonacci mempunyai bentuk yang dibentuk dari fungsi rekursif berikut, ![]() , dengan
, dengan ![]() . Konstruksi fungsi pembangkit untuk barisan Fibonacci sebagai berikut
. Konstruksi fungsi pembangkit untuk barisan Fibonacci sebagai berikut
(1) 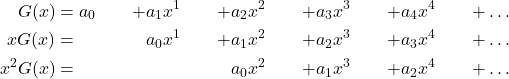
Dari persamaan (1) dikurangi persamaan (2) dan (3), diperoleh
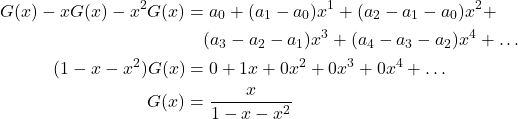
Dengan menggunakan metode pecahan parsial, ![]() dapat dituliskan sebagai
dapat dituliskan sebagai
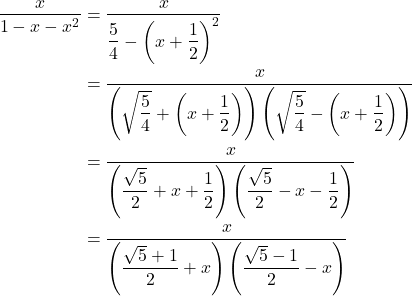
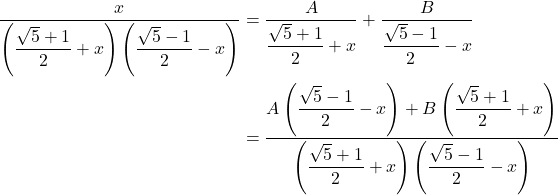
Sehingga, 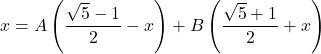 . Dengan memasukkan nilai
. Dengan memasukkan nilai ![]() maka akan didapatkan
maka akan didapatkan
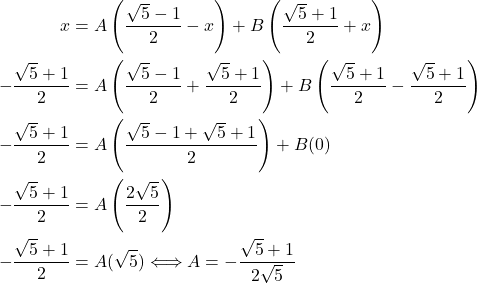
Dengan cara yang sama, dengan memasukkan nilai ![]() maka akan didapatkan
maka akan didapatkan
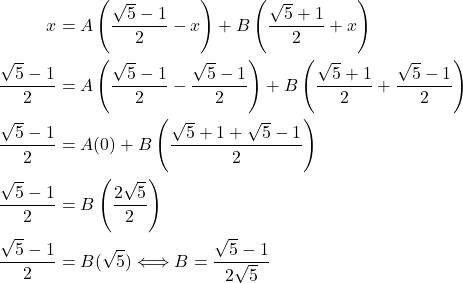
Dengan demikian,
![Rendered by QuickLaTeX.com \begin{align*} \dfrac{x}{1 - x - x^2} & = \dfrac{-\dfrac{\sqrt{5} + 1}{2\sqrt{5}}}{\dfrac{\sqrt{5} + 1}{2} + x} + \dfrac{\dfrac{\sqrt{5} - 1}{2\sqrt{5}}}{\dfrac{\sqrt{5} - 1}{2} - x} \\ & = -\dfrac{\sqrt{5} + 1}{\sqrt{5}(\sqrt{5} + 1) + 2\sqrt{5}x} + \dfrac{\sqrt{5} - 1}{\sqrt{5}(\sqrt{5} - 1) - 2\sqrt{5}x} \\ & = \dfrac{1}{\sqrt{5}}\left[-\dfrac{\sqrt{5} + 1}{\sqrt{5} + 1 + 2x} + \dfrac{\sqrt{5} - 1}{\sqrt{5} - 1 - 2x}\right] \\ & = \dfrac{1}{\sqrt{5}}\left[-\dfrac{\dfrac{\sqrt{5} + 1}{\sqrt{5} + 1}}{\dfrac{\sqrt{5} + 1 + 2x}{\sqrt{5} + 1}} + \dfrac{\dfrac{\sqrt{5} - 1}{\sqrt{5} - 1}}{\dfrac{\sqrt{5} - 1 - 2x}{\sqrt{5} - 1}}\right] \\ \end{align*}](https://matematikadiskrit.mipa.ugm.ac.id/wp-content/ql-cache/quicklatex.com-8dce445c9278c5dff4c9a21569727c8e_l3.png)
![Rendered by QuickLaTeX.com \begin{align*} \dfrac{x}{1 - x - x^2} & = \dfrac{1}{\sqrt{5}}\left[-\dfrac{1}{1 + \dfrac{2}{\sqrt{5} + 1}x} + \dfrac{1}{1 - \dfrac{2}{\sqrt{5} - 1}x}\right] \\ & = \dfrac{1}{\sqrt{5}}\left[-\dfrac{1}{1 + \dfrac{\sqrt{5} - 1}{2}x} + \dfrac{1}{1 - \dfrac{\sqrt{5} + 1}{2}x}\right] \\ & = \dfrac{1}{\sqrt{5}}\left[\dfrac{1}{1 - \dfrac{\sqrt{5} + 1}{2}x} - \dfrac{1}{1 - \dfrac{-\sqrt{5} + 1}{2}x}\right] \end{align*}](https://matematikadiskrit.mipa.ugm.ac.id/wp-content/ql-cache/quicklatex.com-183dfa414532d40975f7e24662d9a76e_l3.png)
Sehingga didapatkan
![Rendered by QuickLaTeX.com \begin{align*} G(x) & = \dfrac{x}{1 - x - x^2} \\ & = \dfrac{1}{\sqrt{5}}\left[\dfrac{1}{1 - \dfrac{\sqrt{5} + 1}{2}x} - \dfrac{1}{1 - \dfrac{-\sqrt{5} + 1}{2}x}\right]. \end{align*}](https://matematikadiskrit.mipa.ugm.ac.id/wp-content/ql-cache/quicklatex.com-31a67b11618ee7eb98b9b988024d6896_l3.png)
Dengan memisalkan
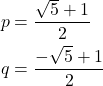
Diperoleh,
![]()
Karena
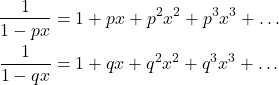
Diperoleh,
![Rendered by QuickLaTeX.com \begin{align*} G(x) & = \dfrac{1}{\sqrt{5}}\left[\dfrac{1}{1 - px} - \dfrac{1}{1 - qx}\right] \\ \sqrt{5}G(x) & = 1 + px + p^2x^2 + p^3x^3 + \dots - (1 + qx + q^2x^2 + q^3x^3 + \dots) \\ \sqrt{5}G(X) & = (1 - 1) + (p - q)x + (p^2 - q^2)x^2 + (p^3 - q^3)x^3 + \dots \\ G(x) & = \dfrac{(1 - 1) + (p - q)x + (p^2 - q^2)x^2 + (p^3 - q^3)x^3 + \dots}{\sqrt{5}} \end{align*}](https://matematikadiskrit.mipa.ugm.ac.id/wp-content/ql-cache/quicklatex.com-4814aec36e7fc6247a97c6e84d09ce24_l3.png)
Jelas bahwa
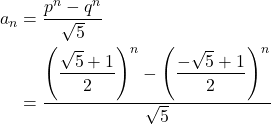
Sehingga bentuk umum dari barisan Fibonacci adalah
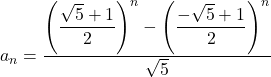
Credit: Ramadhani Latief Firmansyah
Video Penjelasan:
