Misalkan ![]() dan
dan ![]() himpunan dengan banyak anggota berhingga. Pada materi logika matematika dan himpunan telah dikenal beberapa sifat berikut:
himpunan dengan banyak anggota berhingga. Pada materi logika matematika dan himpunan telah dikenal beberapa sifat berikut:
- Kardinalitas himpunan
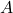 dengan notasi
dengan notasi 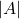 atau
atau 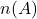 , didefinisikan sebagai banyaknya anggota himpunan
, didefinisikan sebagai banyaknya anggota himpunan 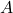 . Sebagai contoh
. Sebagai contoh 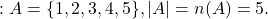
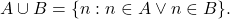
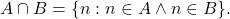
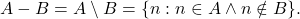
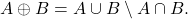
Selanjutnya akan dibahas beberapa sifat lanjutan di ranah himpunan berhingga. Misalkan ![]() dan
dan ![]() suatu himpunan berhingga, maka:
suatu himpunan berhingga, maka:
Selanjutnya diberikan prinsip inklusi-eksklusi yang berasal dari sifat-sifat himpunan yang diperumum. Diberikan himpunan-himpunan ![]() maka berlaku
maka berlaku
![Rendered by QuickLaTeX.com |A_1 \cup A_2 \cup \cdots \cup A_r| = \left[\sum_{i=1}^{r} |A_i| \right] - \left[\sum_{1\leq i < j \leq r} |A_i \cap Aj| \right]](https://matematikadiskrit.mipa.ugm.ac.id/wp-content/ql-cache/quicklatex.com-1fbce3252914a49e105411dd9f9a27b4_l3.png)
![Rendered by QuickLaTeX.com + \left[ \sum_{1 \leq i <j<k\leq r} |A_i \cap A_j \cap A_k|\right]+ \cdots + (-1)^{r-1} |A_1 \cap \cdots \cap A_r|.](https://matematikadiskrit.mipa.ugm.ac.id/wp-content/ql-cache/quicklatex.com-a6fc2295006d21819679fb4f21c0bf7a_l3.png)
- Untuk
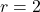 ,
, 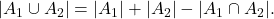
Sebagai contoh soal: Find the number of integers between ![]() and
and ![]() inclusive, that are not divisible by
inclusive, that are not divisible by ![]() and
and ![]()
Didefinisikan
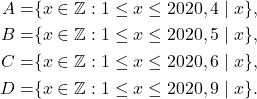
Diperoleh
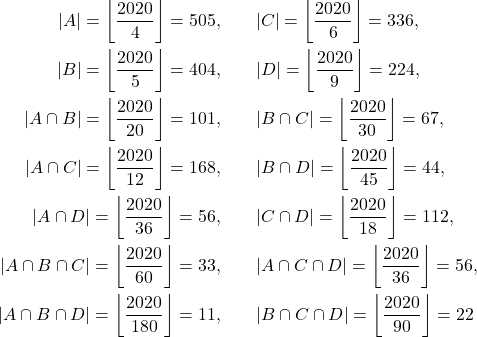
dan
![]()
Jadi banyaknya bilangan bulat ![]()
![]() yang tidak habis dibagi
yang tidak habis dibagi ![]() dan
dan ![]() adalah
adalah
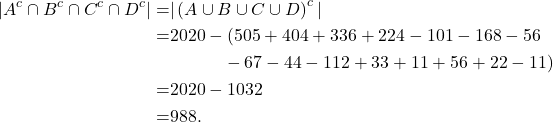
Tutorial: Soal Latihan dan Pembahasan Prinsip Inklusi dan Eksklusi

Komentar