PRINSIP SARANG MERPATI

Download Tayangan

Perhatikan kasus ketika terdapat lebih banyak merpati dibandingkan sarangnya. Sebagai contoh, jika ada 10 merpati yang dimasukkan ke dalam 9 sangkar merpati maka terdapat sangkar yang ditempati oleh setidaknya dua merpati. Secara umum, teorema berikut berlaku.

Teorema. Jika ada (n + 1) merpati yang dimasukkan ke dalam n sangkar merpati, maka terdapat sangkar yang ditempati oleh setidaknya dua merpati.

Bukti. Diketahui ada (n + 1) merpati dan n sangkar. Jika masing-masing sangkar terisi oleh 0 atau 1 (inklusif) merpati saja, maka jumlah total merpati yang telah menempati sangkar hanya sebesar kurang dari n. Dengan demikian, ada lebih dari 1 merpati yang belum masuk ke dalam sangkar. Jika masing-masing kotak hanya diisi oleh 1 ekor merpati, maka jumlah total merpati yang telah menempati sarang ada n merpati dan masih ada 1
merpati yang masih di luar sangkar. Jika 1 merpati tersebut dimasukkan ke dalam salah satu sangkar, maka akan terdapat satu sarang yang terisi oleh 2 (dua) merpati. \square

Pada kasus umum ”merpati” bisa diganti dengan ”obyek”, dan ”sarang merpati” diganti dengan ”perlakuan/penempatan”. Sebagai contoh, akan dipilih 6 bilangan bulat dari himpunan \{1, 2, 3, 4, 5, 6, 7, 8, 9, 10\}. Dapat ditunjukkan bahwa bagaimanapun cara pengambilannya, selalu terdapat 2 bilangan yang jumlahnya adalah 11. Hal ini dapat dilihat dari algoritma berikut:

  • Pasangan bilangan yang jumlahnya 11 adalah

        \[(1, 10), (2, 9) (3, 8) , (4, 7) (5, 6).\]

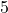  • Ada 5 pasang bilangan yang setiap pasangnya berjumlah 11.
  • Menggunakan analogi sarang merpati, terdapat 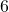6 merpati yang akan menempati 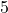5 sarang.
  • Hal ini sama saja mengatakan bahwa dari 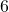6 bilangan yang dipilih pasti ada dua bilangan yang berpasangan.

Terbukti bahwa ada 2 bilangan yang jumlahnya 11.

Tutorial: Soal Latihan dan Pembahasan Prinsip Sarang Merpati