Soal: A bakery sells chocolate, cinnamon, and plain doughnuts and at a particular time has ![]() chocolate,
chocolate, ![]() cinnamon, and
cinnamon, and ![]() plain. If a box contains
plain. If a box contains ![]() doughnuts, how many different option are there for a box of doughnuts?
doughnuts, how many different option are there for a box of doughnuts?
Pembahasan:
Dari informasi pada soal, didapat multiset ![]() , dengan
, dengan ![]() adalah coklat,
adalah coklat, ![]() adalah cinnamon,
adalah cinnamon, ![]() plain. Akan dicari banyaknya solusi dari
plain. Akan dicari banyaknya solusi dari
![]()
dengan ![]()
Dinotasikan
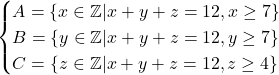
- Untuk
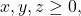 menurut Stars and Bars theorem, diperoleh banyaknya solusi, yaitu
menurut Stars and Bars theorem, diperoleh banyaknya solusi, yaitu
![Rendered by QuickLaTeX.com \[|S| =\binom{3+12-1}{12} = \binom{14}{12} = 91 .\]](https://matematikadiskrit.mipa.ugm.ac.id/wp-content/ql-cache/quicklatex.com-3d3e6888119bc8ba12eca17a3761922c_l3.png)
Untuk memperoleh himpunan
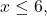
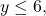
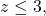 yaitu irisan dari negasi ketiga himpunan tersebut. Dinotasikan
yaitu irisan dari negasi ketiga himpunan tersebut. Dinotasikan![Rendered by QuickLaTeX.com \[|A^{c}\cap B^{c} \cap C^{c}| .\]](https://matematikadiskrit.mipa.ugm.ac.id/wp-content/ql-cache/quicklatex.com-f0b00499b6bf4a315fa5f59901998938_l3.png)
Dengan Prinsip Inklusi-Eksklusi, akan ditentukan banyak solusinya dari
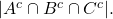
Diperoleh,![Rendered by QuickLaTeX.com \[|A^{c} \cap B^{c} \cap C^{c}| = |S| - |A| - |B| - |C| + |A \cap B| + |A \cap C| + |B \cap C | - | A \cap B \cap C|.\]](https://matematikadiskrit.mipa.ugm.ac.id/wp-content/ql-cache/quicklatex.com-75fc5d2c021b3a521a61df66562dc907_l3.png)
- Selanjutnya, akan dicari solusi
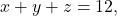 dengan kendala
dengan kendala
![Rendered by QuickLaTeX.com \[\begin{array}{cc} x \geq 7 \\ (x-5) \geq 0 \\ x_1 \geq 0, \text{untuk} \ x_1 = x-7 \end{array}.\]](https://matematikadiskrit.mipa.ugm.ac.id/wp-content/ql-cache/quicklatex.com-aff4a7472a04caa00f21afe68a5ddc47_l3.png)
Maka,
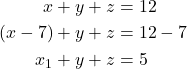
Untuk
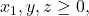 menurut Stars and Bars Theorem, diperoleh banyaknya solusi yaitu
menurut Stars and Bars Theorem, diperoleh banyaknya solusi yaitu![Rendered by QuickLaTeX.com \[|A| = \binom{5+3-1}{5} = \binom{7}{5} = 21.\]](https://matematikadiskrit.mipa.ugm.ac.id/wp-content/ql-cache/quicklatex.com-ac38241f71c6e7d085685933bc5dc1df_l3.png)
- Solusi
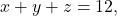 dengan kendala
dengan kendala
![Rendered by QuickLaTeX.com \[\begin{array}{cc} y \geq 7 \\ (y-7) \geq 0 \\ y_1 \geq 0, \text{untuk} \ y_1 = y-7 \end{array}.\]](https://matematikadiskrit.mipa.ugm.ac.id/wp-content/ql-cache/quicklatex.com-663b6dc7c870afab9894480d5c584d61_l3.png)
Maka,
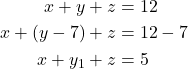
Untuk
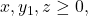 menurut Stars and Bars Theorem, diperoleh banyaknya solusi yaitu
menurut Stars and Bars Theorem, diperoleh banyaknya solusi yaitu![Rendered by QuickLaTeX.com \[|B| = \binom{5+3-1}{5} = \binom{7}{5} = 21.\]](https://matematikadiskrit.mipa.ugm.ac.id/wp-content/ql-cache/quicklatex.com-fe38e061152a71572c4658723da47d7f_l3.png)
- Solusi
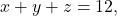 dengan kendala
dengan kendala
![Rendered by QuickLaTeX.com \[\begin{array}{cc} z \geq 4 \\ (z-4) \geq 0 \\ z_1 \geq 0, \text{untuk} \ z_1 = z-4 \end{array}.\]](https://matematikadiskrit.mipa.ugm.ac.id/wp-content/ql-cache/quicklatex.com-bf06ab24a412bb9642c669a6e102a30d_l3.png)
Maka,
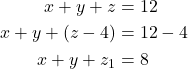
Untuk
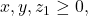 menurut Stars and Bars Theorem, diperoleh banyaknya solusi yaitu
menurut Stars and Bars Theorem, diperoleh banyaknya solusi yaitu![Rendered by QuickLaTeX.com \[|C| = \binom{8+3-1}{8} = \binom{10}{8} = 45.\]](https://matematikadiskrit.mipa.ugm.ac.id/wp-content/ql-cache/quicklatex.com-ef639e211931425570fa7c2cf5b6a76d_l3.png)
- Solusi
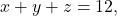 dengan kendala
dengan kendala
![Rendered by QuickLaTeX.com \[\begin{array}{cc} x \geq 7, y \geq 7 \\ (x-5) \geq 0, (y-7) \geq 0 \\ x_1 \geq 0,y_1 \geq 0, \text{untuk} \ x_1 = x-7 , y_1 = y-7 \end{array}.\]](https://matematikadiskrit.mipa.ugm.ac.id/wp-content/ql-cache/quicklatex.com-5f004a65100b64a3bcb3bee5b0e00866_l3.png)
Maka,
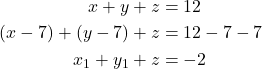
Diperhatikan bahwa,
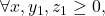 berlaku
berlaku 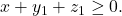 Sedangkan, pernyataan awal akan ditentukan banyaknya solusi
Sedangkan, pernyataan awal akan ditentukan banyaknya solusi 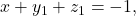 dengan
dengan 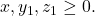 Akibatnya, diperoleh
Akibatnya, diperoleh 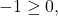 kontradiksi dengan pernyataan awal dimana
kontradiksi dengan pernyataan awal dimana 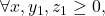 berlaku
berlaku 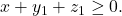 Dengan demikian, banyaknya solusi
Dengan demikian, banyaknya solusi
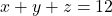 dengan kendala
dengan kendala 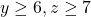 yaitu
yaitu![Rendered by QuickLaTeX.com \[|A \cap B |=0.\]](https://matematikadiskrit.mipa.ugm.ac.id/wp-content/ql-cache/quicklatex.com-a7f67fffbeb77da29e27d6a3c98ced84_l3.png)
- Solusi
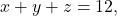 dengan kendala
dengan kendala
![Rendered by QuickLaTeX.com \[\begin{array}{cc} x \geq 7, z \geq 4 \\ (x-7) \geq 0, (z-4) \geq 0 \\ x_1 \geq 0,z_1 \geq 0, \text{untuk} \ x_1 = x-7 , z_1 = z-4 \end{array}.\]](https://matematikadiskrit.mipa.ugm.ac.id/wp-content/ql-cache/quicklatex.com-c088f70697858811cc5abfbedc09e6ca_l3.png)
Maka,
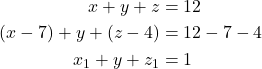
Untuk
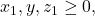 menurut Stars and Bars Theorem, diperoleh banyaknya solusi yaitu
menurut Stars and Bars Theorem, diperoleh banyaknya solusi yaitu![Rendered by QuickLaTeX.com \[|A \cap C| = \binom{3+1-1}{1} = \binom{3}{1} = 3.\]](https://matematikadiskrit.mipa.ugm.ac.id/wp-content/ql-cache/quicklatex.com-6b31f73c9acd69285ee1fcaac3b047ec_l3.png)
- Solusi
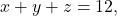 dengan kendala
dengan kendala
![Rendered by QuickLaTeX.com \[\begin{array}{cc} y \geq 7, z \geq 4 \\ (y-7) \geq 0, (z-4) \geq 0 \\ y_1 \geq 0,z_1 \geq 0, \text{untuk} \ y_1 = y-7 , z_1 = z-4 \end{array}.\]](https://matematikadiskrit.mipa.ugm.ac.id/wp-content/ql-cache/quicklatex.com-03b2a77d27a55d3021ce083cd0ff40db_l3.png)
Maka,
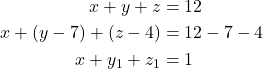
Untuk
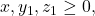 menurut Stars and Bars Theorem, diperoleh banyaknya solusi yaitu
menurut Stars and Bars Theorem, diperoleh banyaknya solusi yaitu![Rendered by QuickLaTeX.com \[|B \cap C| = \binom{3+1-1}{1} = \binom{3}{1} = 3.\]](https://matematikadiskrit.mipa.ugm.ac.id/wp-content/ql-cache/quicklatex.com-797c98ac1d50255822be558941d38e58_l3.png)
- Solusi
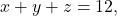 dengan kendala
dengan kendala
![Rendered by QuickLaTeX.com \[\begin{array}{cc} x\geq 7, y \geq 7, z \geq 4 \\ (x-7)\geq 0, (y-7) \geq 0, (z-4) \geq 0 \\ x_1\geq 0, y_1 \geq 0,z_1 \geq 0, \text{ untuk } \ x_1 = x - 7, y_1 = y-7 , z_1 = z-4 \end{array}.\]](https://matematikadiskrit.mipa.ugm.ac.id/wp-content/ql-cache/quicklatex.com-592819d6243e57297a5d2753fdb70a01_l3.png)
Maka,
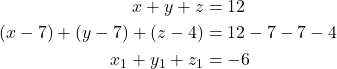
Diperhatikan bahwa,
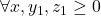 berlaku
berlaku 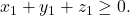 Sedangkan, pernyataan awal akan ditentukan banyaknya solusi
Sedangkan, pernyataan awal akan ditentukan banyaknya solusi 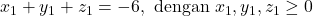
Akibatnya, diperoleh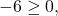 kontradiksi dengan pernyataan awal dimana
kontradiksi dengan pernyataan awal dimana 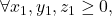 berlaku
berlaku 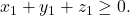
Dengan demikian, banyaknya penyelesaian
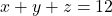 dengan kendala
dengan kendala 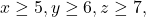 yaitu
yaitu![Rendered by QuickLaTeX.com \[|A \cap B \cap C|=0.\]](https://matematikadiskrit.mipa.ugm.ac.id/wp-content/ql-cache/quicklatex.com-ca1048cff73679cb2adb5e2ccf5d0bf8_l3.png)
Dengan menggunakan Prinsip Inklusi-Eksklusi, diperoleh
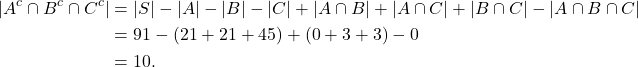
Jadi banyaknya solusi dari ![]() dengan kendala
dengan kendala ![]()
![]()
![]() yaitu sebanyak 10 solusi unik.
yaitu sebanyak 10 solusi unik.
Credit: Fadhlan Zhaahiran
