
Soal Diambil barisan Fibonacci ![]() . Tentukan formula untuk
. Tentukan formula untuk ![]() !
!
Pembahasan
Perhatikan bahwa relasi rekurensi yang dipenuhi adalah ![]() . Selanjutnya dapat dicek juga persamaan polinomial yang dipenuhi adalah
. Selanjutnya dapat dicek juga persamaan polinomial yang dipenuhi adalah
![]()
Jadi ketika dihitung akar-akar karakteristiknya akan menghasilkan
![]()
Jadi ![]() dengan
dengan ![]() . Jika dikembalikan ke rumus umumnya menghasilkan
. Jika dikembalikan ke rumus umumnya menghasilkan
![Rendered by QuickLaTeX.com \[ F_{n} = A_{1}r_{1}^{n} + A_{2}r_{2}^{n} = A_{1}\left(\frac{1}{2} - \frac{\sqrt{5}}{2}\right)^{n} + A_{2}\left(\frac{1}{2} +\frac{\sqrt{5}}{2}\right)^{n} .\]](https://matematikadiskrit.mipa.ugm.ac.id/wp-content/ql-cache/quicklatex.com-bc1e184aafdfbd270de6b7f086ed102b_l3.png)
Selanjutnya nilai awal disubstitusikan ke persamaan di atas, menghasilkan:
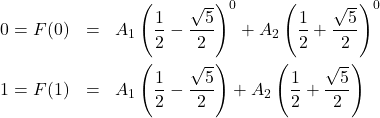
Diperoleh
![]()
Jadi
![]()
Credit: Iwan Ernanto
