
Soal
Suppose that a valid codeword is an ![]() -digit number in decimal notation containing an even number of 0s. Let
-digit number in decimal notation containing an even number of 0s. Let ![]() denote the number of valid codewords of length
denote the number of valid codewords of length ![]() . In Example 3 we showed that the sequence
. In Example 3 we showed that the sequence ![]() satisfies the recurrence relation
satisfies the recurrence relation ![]() and the initial condition
and the initial condition ![]() . Use generating functions to find an explicit formula for
. Use generating functions to find an explicit formula for ![]() .
.
Pembahasan
Untuk membuat pekerjaan dengan fungsi pembangkit lebih sederhana dan mudah, diperluas barisan ini dengan menetapkan ![]() ; ketika ditetapkan nilai ini ke
; ketika ditetapkan nilai ini ke ![]() dan menggunakan relasi rekurensi (perulangan), didapatkan
dan menggunakan relasi rekurensi (perulangan), didapatkan ![]() , yang konsisten dengan kondisi awal. (Hal ini juga masuk akal karena ada satu kata kode dengan panjang 0—string kosong.) Dengan mengalikan kedua sisi relasi rekurensi (pengulangan) dengan
, yang konsisten dengan kondisi awal. (Hal ini juga masuk akal karena ada satu kata kode dengan panjang 0—string kosong.) Dengan mengalikan kedua sisi relasi rekurensi (pengulangan) dengan ![]() akan didapatkan
akan didapatkan ![]() .
.
Misalkan ![]() adalah fungsi pembangkit dari barisan
adalah fungsi pembangkit dari barisan ![]() . Dengan menjumlahkan kedua ruas sisi persamaan terakhir yang dimulai dengan
. Dengan menjumlahkan kedua ruas sisi persamaan terakhir yang dimulai dengan ![]() , didapatkan bahwa
, didapatkan bahwa
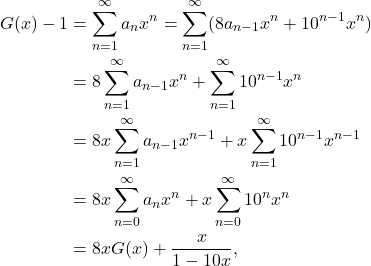
di mana telah digunakan contoh 4 (Fungsi ![]() adalah fungsi pembangkit dari barisan
adalah fungsi pembangkit dari barisan ![]() , karena
, karena ![]() ketika
ketika ![]() , atau ekuivalennya, untuk
, atau ekuivalennya, untuk ![]() untuk
untuk ![]() .) untuk mengevaluasi penjumlahan kedua. Oleh karena itu, didapatkan
.) untuk mengevaluasi penjumlahan kedua. Oleh karena itu, didapatkan ![]() . Pemecahan untuk
. Pemecahan untuk ![]() menunjukkan bahwa
menunjukkan bahwa
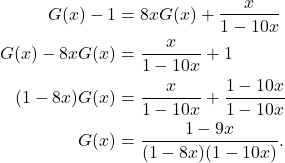
Memperluas ruas kanan persamaan ini menjadi ke dalam bentuk pecahan parsial memberikan
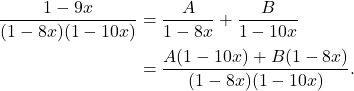
Sehingga, ![]() . Dengan memasukkan nilai
. Dengan memasukkan nilai ![]() maka akan didapatkan
maka akan didapatkan
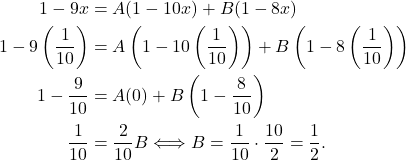
Dengan cara yang sama, dengan memasukkan nilai ![]() maka akan didapatkan
maka akan didapatkan
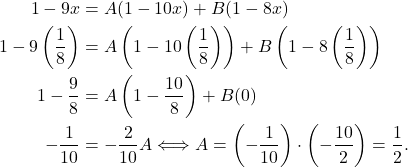
Dengan demikian, 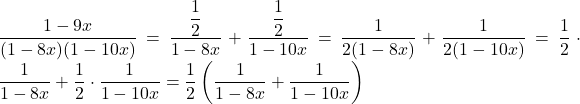 .
.
Sehingga didapatkan ![]() . Menggunakan contoh 4 dua kali (sekali dengan
. Menggunakan contoh 4 dua kali (sekali dengan ![]() dan sekali dengan
dan sekali dengan ![]() ) menghasilkan
) menghasilkan
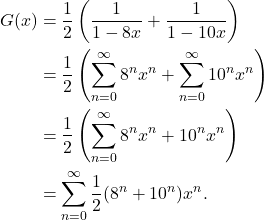
Akibatnya, telah ditunjukkan bahwa ![]() .
.
Credit: Ramadhani Latief Firmansyah
Video Penjelasan:
