Pos oleh :

isnainiuha

Pembahasan Soal 6 Relasi Rekurensi

Tutorial Jumat, 29 Oktober 2021

Soal Solve the recurrence relation

    \[a_{n}=3a_{n-1}-2a_{n-2}+4n\cdot 3^{n},\]

with initial conditions a_{0} = -44, a_{1} = -78.

Pembahasan

Diberikan relasi rekurensi

    \[a_{n}=3a_{n-1}-2a_{n-2}+4n\cdot 3^{n},\]

dengan nilai awal a_{0} = -44, a_{1} = -78.
Diperhatikan bahwa polinomial karakteristik rekurensi linear homogen yang berkorespondensi dengan relasi rekurensi tersebut adalah

    \[p(x)=x^{2}-3x+2=(x-1)(x-2)\]

dengan akar-akarnya adalah 1 dan 2. Dengan demikian solusi homogennya mempunyai bentuk

    \[a_{n}^{(h)}=A+B2^{n}\]

untuk suatu bilangan real A dan B.

Selanjutnya, mengingat f(n)=4n\cdot 3^{n} dan 3 bukan akar dari polinomial karakteristik p(x), maka solusi parsialnya mmiliki bentuk read more

Aljabar Linear

Uncategorized Rabu, 13 Oktober 2021

Aljabar linear adalah bidang studi matematika yang mempelajari sistem persamaan linear dan solusinya, vektor, serta transformasi linear. Matriks dan operasinya juga merupakan hal yang berkaitan erat dengan bidang aljabar linear.

Berikut ini beberapa jurnal khusus yang memuat artikel terkait aljabar linear:

  1. Linear Algebra and its Applications
  2. The Electronic Journal of Linear Algebra

Beberapa artikel civitas akademika UGM terkait aljabar linear:

2020,

Representasi Nilai Eigen Matriks atas Aljabar Maks-Plus Tersimetri dengan ELCP read more

Virtual Tour FMIPA UGM (360 Video)

Artikel Selasa, 31 Agustus 2021

Fakultas yang mengasuh Matematika dan Ilmu Pengetahuan Alam di Universitas Gadjah Mada diresmikan berdirinya pada tanggal 19 September 1955 dengan Surat Keputusan Menteri Pendidikan, Pengajaran dan Kebudayaan tanggal 15 September 1955 nomor 53759/Kab. Saat ini kampus FMIPA dijadikan satu yang berada di Sekip Utara Bulaksumur Yogyakarta. Di video ini kita akan diajak oleh salah satu mahasiswa matematika, yaitu Silvina Rosita Yulianti untuk keliling FMIPA UGM.

Pembahasan Soal 5 Relasi Rekurensi

Tutorial Selasa, 24 Agustus 2021

Soal Diberikan barisan \{a_{n}\} dengan relasi rekurensi a_{n+2}=4a_{n+1}-4a_{n} untuk n\geq 0 dan nilai awal a_{0}=3 dan a_{1}=7. Tentukan formula untuk a_n.

Pembahasan

Persamaan karakteristik yang bersesuaian adalah p(x) = x^{2}-4x+4. Diperoleh k = 2, m_{1} = 2, r_{1} = 2 yang menghasilkan

    \[ a_{n} = (A_{0}+A_{1}n)2^{n} .\]

Dari nilai awal, ketika disubstitusi menjadi

    \begin{equation*} \begin{split} 3 = a_{0} &= A_{0}\\ 10= a_{1}&=2A_{0}+2A_{1}. \end{split} \end{equation*}

Diperoleh

    \begin{equation*} A_{0}=3~\text{dan}~A_{1}=2. \end{equation*}

Jadi a_{n}=(A_{0}+A_{1}n)2^{n}=(3+2n)2^{n}=3\cdot2^{n}+n\cdot2^{n+1} untuk setiap n\geq 0.

Credit: Iwan Ernanto

Pembahasan Soal 4 Relasi Rekurensi

Tutorial Selasa, 24 Agustus 2021

Soal Diberikan barisan \{a_{n}\} dengan relasi rekurensi a_{n+2}=2a_{n+1}-a_{n} untuk n\geq 0 dan nilai awal a_{0}=3 dan a_{1}=7. Tentukan formula untuk a_n.

Pembahasan

Dapat dilihat persamaan karakteristik yang memenuhi adalah p(x) = x^{2}-2x+1. Diperoleh k = 2, m_{1} = 2, r_{1} = 1. Hal ini mengakibatkan

    \[ a_{n} = (A_{0}+A_{1}n)1^{n} .\]

    \begin{equation*} \begin{split} 3 = a_{0} &= A_{0}\\ 7= a_{1}&=A_{0}+A_{1}. \end{split} \end{equation*}

Diperoleh

    \begin{equation*} A_{0}=3~\text{dan}~A_{1}=4 . \end{equation*}

Jadi a_{n}=(A_{0}+A_{1}n)1^{n}=3+4n untuk setiap n\geq 0.

Credit: Iwan Ernanto

Pembahasan Soal 3 Relasi Rekurensi

Tutorial Senin, 23 Agustus 2021

Soal Diberikan barisan \{a_{n}\} dengan relasi rekurensi a_{n + 2} = 5a_{n+1}-4a_{n} untuk n\geq 0 dan a_{0} = 1, a_{2}=7. Tentukan formula untuk a_n.

Jawaban

Persamaan karakteristik yang dihasilkan adalah p(x) = x^{2}-5x+4. Diperoleh k = 2, m_{1} =m_{2}= 1, r_{1} = 1 dan r_{2}=4. Jadi formula untuk a_n adalah

    \[ a_{n} = A_{1}1^{n}+A_{2}4^{n} \]

Dengan mensubstitusi nilai awal akan dihasilkan

    \begin{equation*} \begin{split} 1 = a_{0} &= A_{1}+A_{2}\\ 7= a_{1}&=A_{1}+4A_{2}. \end{split} \end{equation*}

Diperoleh

    \begin{equation*} A_{1}=-1~\text{dan}~A_{2}=2. \end{equation*}

Jadi a_{n}=(-1)\cdot1^{n}+2\cdot 4^{n}=2\cdot 4^{n}-1 untuk setiap n\geq 0.

Credit: Iwan Ernanto

Pembahasan Soal 2 Relasi Rekurensi

Tutorial Senin, 23 Agustus 2021

Soal Diambil barisan Fibonacci \{ F_{n} \} = 0,1, 1, 2, 3, 5, 8, 13, \ldots. Tentukan formula untuk F_n!

Pembahasan

Perhatikan bahwa relasi rekurensi yang dipenuhi adalah F_{n + 2} = F_{n + 1} + F_{n}. Selanjutnya dapat dicek juga persamaan polinomial yang dipenuhi adalah

    \[ x^{2} - x - 1 .\]

Jadi ketika dihitung akar-akar karakteristiknya akan menghasilkan

    \[ r_{1}, r_{2} = \frac{1 \pm \sqrt{1 - 4(-1)}}{2} = \frac{1}{2} \pm\frac{\sqrt{5}}{2} .\]

Jadi k = 2 dengan m_{1} = 1 = m_{2}. Jika dikembalikan ke rumus umumnya menghasilkan

    \[ F_{n} = A_{1}r_{1}^{n} + A_{2}r_{2}^{n} = A_{1}\left(\frac{1}{2} - \frac{\sqrt{5}}{2}\right)^{n} + A_{2}\left(\frac{1}{2} +\frac{\sqrt{5}}{2}\right)^{n} .\]

Selanjutnya nilai awal disubstitusikan ke persamaan di atas, menghasilkan:

    \begin{eqnarray*} 0 = F(0) & = & A_{1}\left(\frac{1}{2} - \frac{\sqrt{5}}{2}\right)^{0} + A_{2}\left(\frac{1}{2} +\frac{\sqrt{5}}{2}\right)^{0}\\ 1 = F(1) & = & A_{1}\left(\frac{1}{2} - \frac{\sqrt{5}}{2}\right) + A_{2}\left(\frac{1}{2} +\frac{\sqrt{5}}{2}\right) \end{eqnarray*} read more

Pembahasan Soal 1 Relasi Rekurensi

Tutorial Senin, 23 Agustus 2021

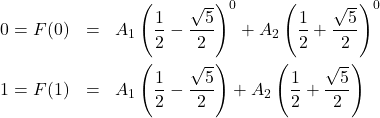
Soal: Diberikan barisan \{a_{n}\} dengan relasi rekurensi a_{n + 1} = 2a_{n} dan a_{0} = 1. Carilah formula dari a_n!

Pembahasan:

Persamaan karakteristik p(x) = x - 2. Diperoleh k = 1, m_{1} = 1, dan r_{1} = 2. Jadi,

    \[ a_{n} = A_{1}2^{n} .\]

Dari nilai awal ketika disubstitusi diperoleh

    \[ n = 0 \mapsto 1 = a_{0} = A_{1}2^{0} \Longrightarrow A_{1} = 1 .\]

Hal ini mengakibatkan formula untuk a_n adalah

    \[ a_{n} = 1\cdot 2^{n} = 2^{n} \]

Credit: Iwan Ernanto

Virtual Tour FMIPA UGM

Artikel Minggu, 22 Agustus 2021

Fakultas yang mengasuh Matematika dan Ilmu Pengetahuan Alam di Universitas Gadjah Mada diresmikan berdirinya pada tanggal 19 September 1955 dengan Surat Keputusan Menteri Pendidikan, Pengajaran dan Kebudayaan tanggal 15 September 1955 nomor 53759/Kab. Saat ini kampus FMIPA dijadikan satu yang berada di Sekip Utara Bulaksumur Yogyakarta. Di video ini kita akan diajak oleh salah satu mahasiswa matematika, yaitu Silvina Rosita Yulianti untuk keliling FMIPA UGM.