Pada abad awal ke-13 (tahun 1202), Leonardo da Pisa (beliau lebih dikenal dengan nama Fibo-nacci, yang artinya, “anak Bonaccio”) menuliskan suatu problem dibukunya Liber Abaci (Buku tentang Abacus). Berikut adalah problem yang terdapat pada buku tersebut.
Misalkan pertumbuhan jumlah kelinci mengikuti keadaan sebagai berikut. Sepasang kelinci menjadi dewasa dalam waktu satu bulan, dan setiap bulan berikutnya berturut-turut setiap bulan melahirkan sepasang anak kelinci, jantan dan betina. Pada awal tahun, ada sepasang anak kelinci. Jika diasumsikan tidak ada kelinci yang mati, berapakah jumlah pasangan kelinci itu setelah satu tahun?
Tentunya terdapat pola dari banyaknya kelinci pada suatu waktu. Selanjutnya Barisan Fibonacci ![]() didefinisikan dengan kondisi awal
didefinisikan dengan kondisi awal
![]()
dan relasi rekurensi
![]()
Barisan rekurensi ini merupakan barisan rekurensi linear berorder ![]() . Selanjutnya dapat dicari rumus eksplisit untuk
. Selanjutnya dapat dicari rumus eksplisit untuk ![]() adalah
adalah
![]()
Selanjutnya akan dibahas salah satu sifat Barisan Fibonacci. Diberikan barisan Fibonacci ![]()
![]()
Diperhatikan bahwa
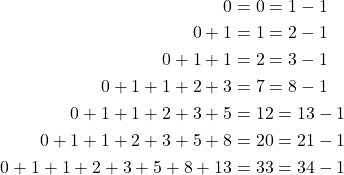
Akan ditunjukkan bahwa
![]()
Akan ditunjukkan persamaan tersebut menggunakan induksi matematika.
- Sudah dibuktikan bahwa untuk
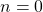 dan
dan 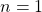 pernyataan di atas benar.
pernyataan di atas benar. - Diasumsikan benar untuk
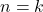 , yakni
, yakni
![Rendered by QuickLaTeX.com \[F_{0}+F_{1}+F_{2}+\cdots+F_{k}=F_{k+2}-1\]](https://matematikadiskrit.mipa.ugm.ac.id/wp-content/ql-cache/quicklatex.com-de925263cc7bd6dd3d7db82860456d5d_l3.png)
- Dibuktikan benar untuk
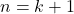 , yakni
, yakni
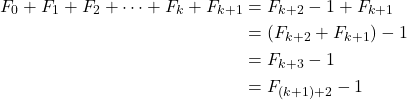
Berdasarkan prinsip induksi matematika, untuk setiap ![]() berlaku
berlaku
![]()

Komentar