Soal
Diberikan lapangan hingga dengan banyak anggota 8 yang dikontruksikan dari irreducible polynomial ![]() atas
atas ![]() :
:
- Buktikan bahwa
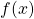 irreducible pada
irreducible pada ![Rendered by QuickLaTeX.com GF(2)[x]](https://matematikadiskrit.mipa.ugm.ac.id/wp-content/ql-cache/quicklatex.com-186339eed945e3a8e304fa9a383ac1aa_l3.png)
- Jika
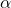 merupakan akar dari
merupakan akar dari 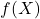 , cari elemen-elemen lapangan polinomialnya
, cari elemen-elemen lapangan polinomialnya - Konstruksikan tabel Zech’s log untuk lapangan tersebut
Pembahasan
Diberikan ![]() atas
atas ![]()
\begin{enumerate}[(a)]
\item \textbf{Cara 1}: Andaikan ![]() reducible atas
reducible atas ![]() , artinya terdapat
, artinya terdapat ![]() yang memenuhi
yang memenuhi
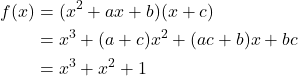
Akibatnya, diperoleh persamaan-persamaan berikut
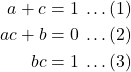
Diperhatikan bahwa dari persamaan ![]() yaitu
yaitu ![]() , diperoleh
, diperoleh ![]() . Selanjutnya,
. Selanjutnya, ![]() disubstitusikan ke persamaan
disubstitusikan ke persamaan ![]() , diperoleh
, diperoleh

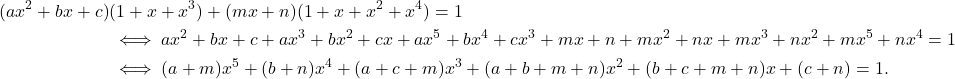
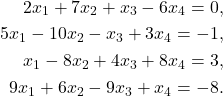
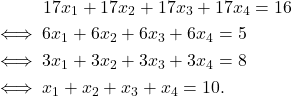
![Rendered by QuickLaTeX.com \begin{align*} (X+Y)+Z&= ((X \cup Y) - (X \cap Y)) + Z\\ &= [((X \cup Y) - (X \cap Y)) \cup Z]\\ &\hspace{0.7cm}-[((X \cup Y) - (X \cap Y)) \cap Z]\\ &=[((X \cup Y) \cap (X \cap Y)^C) \cup Z]\\ &\hspace{0.7cm}-[((X \cup Y) \cap (X \cap Y)^C) \cap Z]\\ &=[(X \cup Y \cup Z) \cap ((X \cap Y)^C \cup Z)]\\ &\hspace{0.7cm}-[((X \cup Y) \cap (X \cap Y)^C) \cap Z]\\ &=[(X\cup Y\cup Z)\cap (X^C\cup Y^C\cup Z)]\\ &\hspace{0.7cm}-[(X\cup Y)\cap (X^C\cup Y^C)\cap Z]\\ &=[( (X\cap Y^C)\cup (X\cap Z)\cup(Y\cap X^C)\cup\\ &\hspace{0.7cm} (Y\cap Z)\cup (Z\cap X^C)\cup (Z\cap Y^C)\cup Z)\cap \\ &\hspace{0.7cm}-\{\}\\ &\hspace{0.7cm}-[((X\cup Y)\cap (X^C\cup Y^C))\cap Z]\\ &\hspace{0.7cm}....\\ &=[(X \cup ((Y \cup Z) \cap (Y \cap Z)^C))]\\ &\hspace{0.7cm}- [X \cap ((Y \cup Z) \cap (Y \cap Z)^C)]\\ &=[(X \cup ((Y \cup Z) - (Y \cap Z)))]\\ &\hspace{0.7cm}- [X \cap ((Y \cup Z) - (Y \cap Z))]\\ &=X+((Y \cup Z) - (Y \cap Z))\\ &=X+(Y+Z) \end{align*}](https://matematikadiskrit.mipa.ugm.ac.id/wp-content/ql-cache/quicklatex.com-043cffa726d1c9546e560abe6fb0f89b_l3.png)



![Rendered by QuickLaTeX.com \[2^{1+2} | (2p-1)^{2^1}-1 \Leftrightarrow 2^{3} | 4p^2 - 4p$ \Leftrightarrow 2^{3} | 4p(p - 1).\]](https://matematikadiskrit.mipa.ugm.ac.id/wp-content/ql-cache/quicklatex.com-2e492441eefcc3c33ac870e27361a8bc_l3.png)

Komentar