Soal: Tentukan banyaknya bilangan dari ![]() sampai
sampai ![]() yang relatif prima terhadap
yang relatif prima terhadap ![]() .
.
Pembahasan:
Diketahui bahwa pembagi prima dari ![]() yaitu
yaitu ![]() dan
dan ![]() . Selanjutnya, di defenisikan
. Selanjutnya, di defenisikan ![]() adalah himpunan bilangan bulat yang habis dibagi
adalah himpunan bilangan bulat yang habis dibagi ![]() ,
, ![]() adalah himpunan bilangan bulat yang habis dibagi
adalah himpunan bilangan bulat yang habis dibagi ![]() ,
, ![]() adalah himpunan bilangan bulat yang habis dibagi
adalah himpunan bilangan bulat yang habis dibagi ![]() . Akan dicari banyaknya bilangan dari
. Akan dicari banyaknya bilangan dari ![]() sampai
sampai ![]() yang relatif prima terhadap
yang relatif prima terhadap ![]() yaitu
yaitu ![]() .
.
Diperoleh,

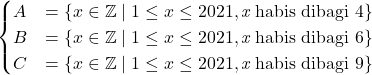
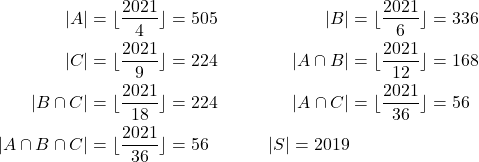
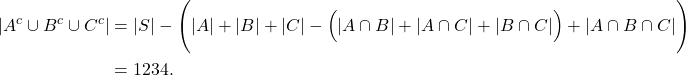
![Rendered by QuickLaTeX.com \[\sum_{k=1}^{n} k(n+1-k) = \binom{n+2}{3} .\]](https://matematikadiskrit.mipa.ugm.ac.id/wp-content/ql-cache/quicklatex.com-9217217be3fb2d77b0611c9c3adce2b4_l3.png)
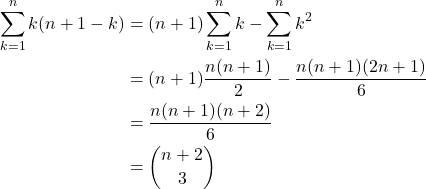
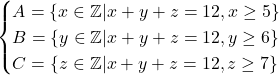
Komentar