FUNGSI DISKRIT NUMERIK

Download Tayangan

Fungsi merupakan relasi biner yang bersifat khusus yaitu setiap anggota domain memiliki tepat satu kawan di kodomain. Fungsi diskrit numerik adalah suatu fungsi dengan himpunan bilangan cacah sebagai domain dan himpunan bilangan riil sebagai kodomainnya. Fungsi jenis ini menjadi pokok bahasan yang menarik karena sering digunakan dalam komputasi digital. Selanjutnya diberikan beberapa contoh fungsi diskrit numerik.
  • Misalkan 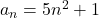a_n = 5n^2 +1, dengan 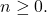n\geq 0. Bentuk ini dapat dipandang sebagai fungsi diskrit numerik.
  • Misalkan

        \[b_n = \begin{cases} 2n&, 0 \leq n \leq 11 \\ 2^n -1 &, n\geq 12\end{cases}.\]

    Dapat dilihat bahwa bentuk ini merupakan fungsi diskrit numerik.

Seperti fungsi pada umumnya, fungsi diskrit numerik dapat dijumlahkan dan juga dikalikan.

Jumlah dari dua fungsi numerik didefinisikan sebagai sebuah fungsi numerik yang petanya

pada n tertentu sama dengan jumlah peta dari kedua fungsi numerik pada n.

Hasil kali juga didefinisikan dengan cara yang sama yaitu peta 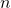n tertentu sama dengan hasil kali peta dari kedua fungsi numerik pada 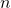n. Dengan demikian dapat dilihat dengan mudah bahwa jumlah dan kali dua fungsi diskrit numerik akan menghasilkan fungsi diskrit numerik.

Tutorial: Soal Latihan dan Pembahasan Fungsi Diskrit Numerik