Pembahasan Soal 1 Prinsip Inklusi-Eksklusi

File Tayangan

Soal: Tentukan banyaknya bilangan bulat dari 1 hingga 2021 yang tidak habis dibagi 4,6, dan 9.

Pembahasan:

Dinotasikan himpunan :

    \begin{align*} \begin{cases} A &= \{x\in\mathbb{Z}\mid 1 \leq x \leq 2021, \textit{x} \ \text{habis dibagi} \ 4 \} \\ B &= \{x\in\mathbb{Z}\mid 1 \leq x \leq 2021, \textit{x} \ \text{habis dibagi} \ 6\} \\ C &= \{x\in\mathbb{Z}\mid 1 \leq x \leq 2021, \textit{x} \ \text{habis dibagi} \ 9\} \end{cases} \end{align*}

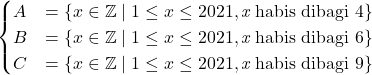
Akan ditentukan banyaknya bilangan bulat antara 1 dan 2021 yang tidak habis dibagi 4,6, dan 9, yaitu |A^{c} \cup B^{c} \cup C^{c}|.
Diperoleh,

    \begin{align*} |A| &= \lfloor\frac{2021}{4}\rfloor =505 & |B| &= \lfloor\frac{2021}{6}\rfloor = 336\\ |C| &= \lfloor\frac{2021}{9}\rfloor = 224 & |A\cap B| &= \lfloor\frac{2021}{12}\rfloor = 168 \\ |B\cap C| &= \lfloor\frac{2021}{18}\rfloor = 224 & |A\cap C| &= \lfloor\frac{2021}{36}\rfloor = 56 \\ |A\cap B \cap C| &= \lfloor\frac{2021}{36}\rfloor = 56 & |S| = 2019 \end{align*}

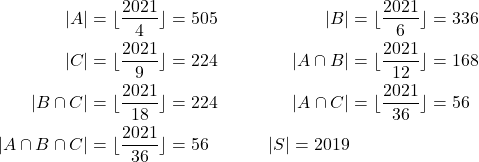
Dengan menggunakan Prinsip Inklusi-Eksklusi, diperoleh

    \begin{align*} |A^{c} \cup B^{c} \cup C^{c}| &= |S| - \Bigg(|A|+|B|+|C|-\Big(|A\cap B|+|A\cap C|+|B \cap C|\Big)+|A\cap B \cap C|\Bigg) \\ &= 1234. \end{align*}

 

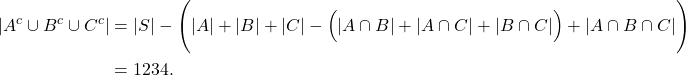
Credit: Fadhlan Zhaahiran

Tinggalkan Balasan ke jiii Batalkan balasan

Alamat email Anda tidak akan dipublikasikan.

*

Comment (2)

  1. jiii 1 years ago

    izin bertanya bapak/ibu, jika soalnya “habis dibagi” apakah jalannya akan sama dengan ini ya pak/bu? terimakasih

    Reply
  2. jiii 1 years ago

    izin bertanya bapak/ibu, jika soalnya “habis dibagi” apakah jalannya akan sama dengan ini ya pak/bu? terimakasih.

    Reply