
Soal Diberikan barisan ![]() yang memenuhi relasi rekurensi
yang memenuhi relasi rekurensi
![]()
untuk setiap ![]() dan dengan suku awal
dan dengan suku awal ![]() . Dengan menggunakan fungsi pembangkit, tentukan formula untuk
. Dengan menggunakan fungsi pembangkit, tentukan formula untuk ![]() .
.
Pembahasan
Dibentuk barisan ![]() dengan
dengan
![]()
untuk setiap ![]() .
.
Diperhatikan bahwa untuk ![]() berlaku
berlaku
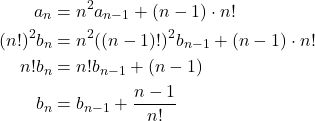
dan ![]() .
.
\newline
Selanjutnya, misalkan ![]() adalah fungsi pembangkit untuk barisan
adalah fungsi pembangkit untuk barisan ![]() . Dengan demikian
. Dengan demikian
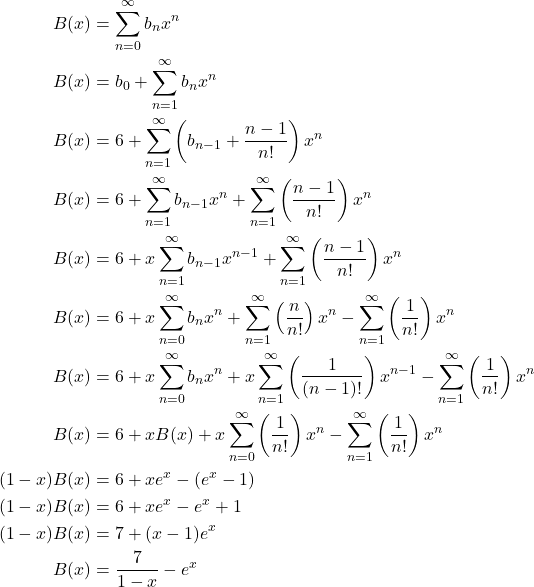
Dengan demikian diperoleh ![]() untuk setiap
untuk setiap ![]() .
.
\newline
Mengingat
![]()
untuk setiap ![]() , diperoleh
, diperoleh
![]()
Credit: Iwan Ernanto
Video Penjelasan:
