Soal
Use generating functions to find the number of ways to select ![]() objects of
objects of ![]() different kinds if we must select at least one object of each kind.
different kinds if we must select at least one object of each kind.
Pembahasan
Karena perlu dipilih setidaknya satu objek dari setiap jenis, masing-masing dari ![]() jenis objek menyumbang faktor
jenis objek menyumbang faktor ![]() ke fungsi pembangkit
ke fungsi pembangkit ![]() untuk barisan
untuk barisan ![]() , dengan
, dengan ![]() adalah banyaknya jumlah cara untuk memilih
adalah banyaknya jumlah cara untuk memilih ![]() objek dari
objek dari ![]() jenis yang berbeda jika dibutuhkan setidaknya satu objek dari setiap jenis. Oleh karena itu,
jenis yang berbeda jika dibutuhkan setidaknya satu objek dari setiap jenis. Oleh karena itu, ![]() . Dengan menggunakan teorema binomial yang diperluas dan contoh 2 yang memberikan rumus sederhana untuk
. Dengan menggunakan teorema binomial yang diperluas dan contoh 2 yang memberikan rumus sederhana untuk ![]() , diperoleh
, diperoleh
Soal
Use generating functions to find the number of ![]() -combinations from a set with
-combinations from a set with ![]() elements when repetition of elements is allowed.
elements when repetition of elements is allowed.
Pembahasan
Misalkan ![]() adalah fungsi pembangkit untuk barisan
adalah fungsi pembangkit untuk barisan ![]() , di mana
, di mana ![]() sama dengan banyaknya jumlah
sama dengan banyaknya jumlah ![]() -kombinasi dari suatu himpunan dengan
-kombinasi dari suatu himpunan dengan ![]() elemen dengan pengulangan yang diperbolehkan. Yaitu,
elemen dengan pengulangan yang diperbolehkan. Yaitu, ![]() . Karena kita dapat memilih sejumlah anggota tertentu dari himpunan dengan
. Karena kita dapat memilih sejumlah anggota tertentu dari himpunan dengan ![]() elemen ketika kita membentuk kombinasi-
elemen ketika kita membentuk kombinasi-![]() dengan pengulangan yang diperbolehkan, masing-masing dari
dengan pengulangan yang diperbolehkan, masing-masing dari ![]() elemen berkontribusi
elemen berkontribusi ![]() pada ekspansi perkalian untuk
pada ekspansi perkalian untuk ![]() . Setiap elemen memberikan kontribusi faktor tersebut karena dapat dipilih nol kali, satu kali, dua kali, tiga kali, dan seterusnya, ketika
. Setiap elemen memberikan kontribusi faktor tersebut karena dapat dipilih nol kali, satu kali, dua kali, tiga kali, dan seterusnya, ketika ![]() -kombinasi terbentuk (dengan total
-kombinasi terbentuk (dengan total ![]() elemen yang dipilih).
elemen yang dipilih).
Soal
Use generating functions to find the number of ![]() -combinations of a set with
-combinations of a set with ![]() elements. Assume that the binomial theorem has already been established.
elements. Assume that the binomial theorem has already been established.
Pembahasan
Masing-masing dari ![]() elemen dalam himpunan menyumbangkan suku
elemen dalam himpunan menyumbangkan suku ![]() ke fungsi pembangkit
ke fungsi pembangkit ![]() . Di sini
. Di sini ![]() adalah fungsi pembangkit untuk
adalah fungsi pembangkit untuk ![]() , di mana
, di mana ![]() menyatakan jumlah banyaknya
menyatakan jumlah banyaknya ![]() -kombinasi dari suatu himpunan dengan
-kombinasi dari suatu himpunan dengan ![]() elemen. Karena itu,
elemen. Karena itu, ![]() . Tetapi dengan teorema binomial, didapatkan
. Tetapi dengan teorema binomial, didapatkan ![]() , dengan
, dengan ![]() . Oleh karena itu,
. Oleh karena itu, ![]() , banyaknya jumlah
, banyaknya jumlah ![]() -kombinasi dari suatu himpunan dengan
-kombinasi dari suatu himpunan dengan ![]() elemen, adalah
elemen, adalah ![]() .
.
Soal
Gunakan fungsi pembangkit untuk mencari banyaknya kombinasi token bernilai ![]() dollar,
dollar, ![]() dollar, and
dollar, and ![]() dollar untuk membayar barang seharga
dollar untuk membayar barang seharga ![]() dollar di mesin penjual (baik memperhatikan urutan, maupun tidak memperhatikan urutan).
dollar di mesin penjual (baik memperhatikan urutan, maupun tidak memperhatikan urutan).
Pembahasan
Pertimbangkan kasus ketika urutan token yang dimasukkan tidak menjadi masalah. Di sini, yang dipedulikan hanyalah jumlah setiap token yang digunakan untuk menghasilkan total ![]() dolar. Karena kita dapat menggunakan sejumlah token
dolar. Karena kita dapat menggunakan sejumlah token ![]() dollar, sejumlah token
dollar, sejumlah token ![]() dollar, dan sejumlah token
dollar, dan sejumlah token ![]() dollar, jawabannya adalah koefisien
dollar, jawabannya adalah koefisien ![]() dalam fungsi pembangkit
dalam fungsi pembangkit
Soal
Berapa banyak cara delapan biskuit dapat diberikan ke 3 anak sehingga setiap anak menerima minimal 2 biskuit dan tidak lebih dari 4 biskuit?
Pembahasan
Karena setiap anak menerima setidaknya paling sedikit dua tetapi tidak lebih dari empat kue, untuk setiap anak ada faktor yang sama dengan ![]() dalam fungsi pembangkit untuk barisan
dalam fungsi pembangkit untuk barisan ![]() , di mana
, di mana ![]() adalah jumlah cara untuk membagikan sebanyak
adalah jumlah cara untuk membagikan sebanyak ![]() buah kue. Karena ada tiga anak, maka fungsi pembangkit ini adalah
buah kue. Karena ada tiga anak, maka fungsi pembangkit ini adalah ![]() . Kita membutuhkan koefisien
. Kita membutuhkan koefisien ![]() dalam hasil kali ini. Alasannya adalah bahwa suku
dalam hasil kali ini. Alasannya adalah bahwa suku ![]() dalam ekspansi sesuai dengan cara pemilihan tiga suku, dengan satu dari setiap faktor, yang memiliki pangkat yang ditambahkan hingga berjumlah 8.
dalam ekspansi sesuai dengan cara pemilihan tiga suku, dengan satu dari setiap faktor, yang memiliki pangkat yang ditambahkan hingga berjumlah 8.
Soal
Carilah banyaknya solusi bulat dari ![]() , dengan
, dengan ![]() ,
, ![]() , and
, and ![]() bilangan bulat tak negatif yang memenuhi
bilangan bulat tak negatif yang memenuhi ![]()
![]() , dan
, dan ![]() .
.
Pembahasan
Banyaknya solusi dengan batasan-batasan yang diberikan adalah koefisien dari ![]() dalam perluasan
dalam perluasan ![]() . Hal ini terjadi karena kita memperoleh suku yang sama dengan
. Hal ini terjadi karena kita memperoleh suku yang sama dengan ![]() pada hasil kali dengan memilih suku pada jumlah pertama
pada hasil kali dengan memilih suku pada jumlah pertama ![]() , suku pada jumlah kedua
, suku pada jumlah kedua ![]() , dan suku pada jumlah ketiga
, dan suku pada jumlah ketiga ![]() , di mana eksponen
, di mana eksponen ![]() ,
, ![]() , dan
, dan ![]() memenuhi persamaan
memenuhi persamaan ![]() dan batasan-batasan yang diberikan. Tidak sulit untuk melihat bahwa koefisien
dan batasan-batasan yang diberikan. Tidak sulit untuk melihat bahwa koefisien ![]() pada hasil kali ini adalah 3. Oleh karena itu, ada tiga solusi.
pada hasil kali ini adalah 3. Oleh karena itu, ada tiga solusi.
Soal
Apakah fungsi pembangkit dari barisan ![]() ?
?
Pembahasan
Fungsi pembangkit dari 1, 1, 1, 1, 1, 1 adalah ![]() . Sehingga dengan teorema jika
. Sehingga dengan teorema jika ![]() dan
dan ![]() adalah bilangan real dan
adalah bilangan real dan ![]() , maka
, maka
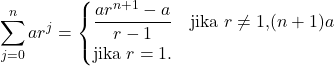
didapatkan ![]() dengan
dengan ![]() . Akibatnya,
. Akibatnya, ![]() adalah fungsi pembangkit dari barisan 1, 1, 1, 1, 1, 1.
adalah fungsi pembangkit dari barisan 1, 1, 1, 1, 1, 1.
[Karena pangkat dari ![]() hanya pemegang tempat untuk suku-suku barisan dalam fungsi pembangkit, kita tidak perlu khawatir bahwa
hanya pemegang tempat untuk suku-suku barisan dalam fungsi pembangkit, kita tidak perlu khawatir bahwa ![]() tidak terdefinisi.].
tidak terdefinisi.].
Credit: Ramadhani Latief Firmansyah
Departemen Matematika FMIPA UGM didirikan pada tanggal 19 September 1955 bersamaan dengan berdirinya fakultas yang mengasuh bidang Matematika dan Ilmu Pengetahuan Alam dengan SK Menteri Pendidikan, Pengajaran dan Kebudayaan No.53759/Kab, tanggal 15 September 1955. Dalam surat keputusan itu disebutkan bahwa fakultas tersebut masih merupakan gabungan dengan Fakultas Teknik sehingga diberi nama Persatuan Fakultas Ilmu Pasti dan Alam dan Fakultas Teknik. Pada saat itu, Fakultas Ilmu Pasti dan Alam baru mempunyai satu bagian yaitu Bagian Ilmu Pasti. Sejak tanggal 1 September 1956, Fakultas Ilmu Pasti dan Alam (disingkat FIPA) mulai memisahkan diri dari Fakultas Teknik.
Soal Diberikan barisan ![]() yang memenuhi relasi rekurensi
yang memenuhi relasi rekurensi
![]()
untuk setiap ![]() dan dengan suku awal
dan dengan suku awal ![]() . Dengan menggunakan fungsi pembangkit, tentukan formula untuk
. Dengan menggunakan fungsi pembangkit, tentukan formula untuk ![]() .
.
Pembahasan
Dibentuk barisan ![]() dengan
dengan
![]()
untuk setiap ![]() .
.
Diperhatikan bahwa untuk ![]() berlaku
berlaku
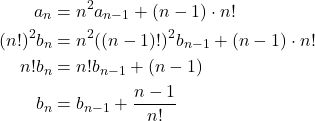
dan ![]() .
.
\newline
Selanjutnya, misalkan ![]() adalah fungsi pembangkit untuk barisan
adalah fungsi pembangkit untuk barisan ![]() . Dengan demikian
. Dengan demikian
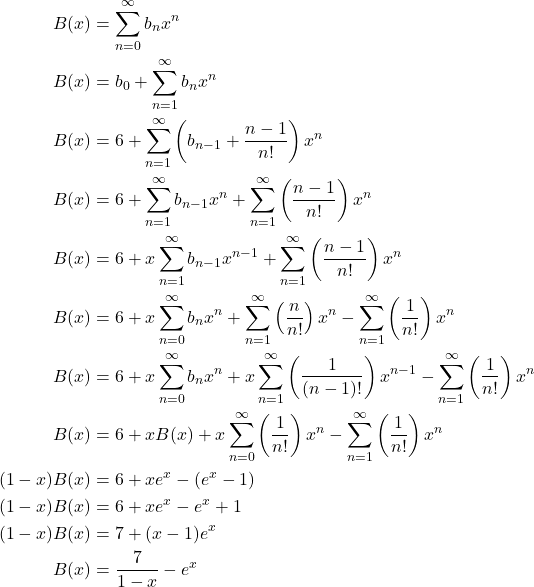
Dengan demikian diperoleh ![]() untuk setiap
untuk setiap ![]() .
.
\newline
Mengingat



Komentar